. Written in this way, we say that is it in matrix form. The way we interpret the form is that when there is a 1, it is replaced by a 3; 2 by 5; 3 by 1; 4 by itself; and 5 by 2.This is an example of a finite permutation: . Written in this way, we say that is it in matrix form. The way we interpret the form is that when there is a 1, it is replaced by a 3; 2 by 5; 3 by 1; 4 by itself; and 5 by 2.
It can also be written in cycle form. An example of a cycle is (1 5 7). This means that 1 is replaced by 5, 5 is replaced by 7, and 7 is replaced by 1. In our example, we can write f as f = (1 3)(2 5)(4). A number that is changed into itself may be omitted from the cycle form. E.g., f=(1 3)(2 5) is the same as f = (1 3)(2 5)(4). Each of the components of the closed form is called an orbit. (1 3) is an orbit.
These permutations do not exhibit commutative properties. For example, if you have two permutations, g=(1 2 3) and h=(1 4)(2 5), gh does not equal hg. (We define gh by first doing the permutation action g and then doing h.)
gh=(1 2 3)(1 4)(2 5)= 
hg=(1 4)(2 5)(1 2 3)=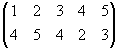 
This example demonstrates that the commutative property do not always apply for permutations (although sometimes it does).
A transposition is a 2-cycle such as (2 5). Every permutation can be written as a product of transpositions. For example: (2 4 3 5) = (2 4)(2 3)(2 5). The product of these transpositions will result in the original permutation.
The set Sn is the set of all permutations over the set {1, 2, 3, …, n}. For example, (1 3 4)(2 5) is a member of S5, but not of S3. The set Sn can be made into an algebraic group by using the multiplication mentioned above. This group is not abelian.
An example of the practical application of finite permutations can be found in the WWII Nazi coding device: the Enigma Machine. The Enigma Machine made use of a series of complicated rotors, a plugboard, and a reflector. Due to the design of the machine, you could think of each state as a member of S26. However, not every permutation on 26 letters were possible, because, for example, if the letter "J" was typed into the machine and it came out as, say "B", but if the letter "B" had been typed instead, then it would have come out as a "J". In other words, each state was the product of 13 transpositions. So here is a possible state of the Enigma Machine, represented as a permutation:
(A C)(B Q)(D R)(E G)(F Z)(H Y)(I J)(K S)(L V)(M X)(N P)(O T)(U W)
And here is an impossible state:
(A B C D E)(F G H J K)(M N I)(T R Q S)(O W)(P V)(U X Y Z L)
This mathematical structure was exploited by the Poles in their work in breaking Enigma.