Spherical and Hyperbolic San Gaku Problems
Previous Research With Undergraduates
Summer 2006
In previous summers I have worked with undergraduates in other areas of geometry. Namely, we worked on extending some theorems and/or definitions from the Euclidean plane to spherical and hyperbolic geometry. There were many possible theorems and definitions that we tried to extend and the students were given some choices.
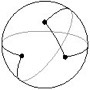
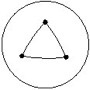
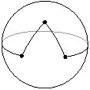
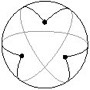
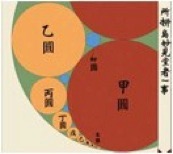
We built on the results of the summer 2004 project. Again we tried to generalize Japanese temple problems to spherical and hyperbolic geometry. Japanese temple problems are ancient Euclidean geometry problems that were inscribed on colorful tablets and hung, as a form of worship, in temples across Japan during the Edo period (1603-1867). Below is an example of this type of problem:
We began by learning about spherical geometry and reviewing the results from summer 2004. Initially, we extended the Euclidean inscribed angle theorem to a weaker result on the sphere involving bounds on the inscribed angle. Then we extended some of those San Gaku problems that involved parallel Euclidean lines in multiple ways to spherical geometry. In addition, using the same strategy as in spherical geometry, we extended a few of the San Gaku problems involving parallel lines to hyperbolic geometry with hyperparallel lines.
Along the way we learned a lot of spherical and hyperbolic trigonometry from a text book that is over 100 year old! (Do you remember the law of sines or cosines from the Euclidean plane? Well there are spherical and hyperbolic analogs of those.) We also learned about a model of hyperbolic geometry which leads to many notions in modern differential geometry. Also, to help explore spherical conjectures, we used the program that David Austin and I wrote called Spherical Easel. Check this program out.
Spherical and Hyperbolic Geometry
Summer 2004
Over this summer I worked two students to extend some theorems from the Euclidean plane. We first worked with inversion in the plane tried to understand inversion on the sphere. We attempted use inversion on the sphere to mirror constructions of geometric arrangements of circles and line from the Euclidean plane on the sphere. When this turned out not to be so successful, we turned our attention to a type of ancient Japanese temple problem in the Euclidean plane. Many of these problems involved ellipses and therefore we had to understand what ellipses were on the surface of the sphere. We were very successful in characterizing ellipses (using the definition of the sum of the distances from two foci is constant) on the surface of the sphere and later in the hyperbolic plane. This allowed us to generalize a Japanese temple problem that we called the flower problem on the sphere and in the hyperbolic plane. This is pictured below.
We classified all the trilaterals on the sphere and examined when the triangle theorems extend to the sphere. In general we found that most triangle theorems do not extend, unless you restrict the type of trilaterals. Our results were published in The Pi Mu Epsilon Journal in the Spring 2005 edition.
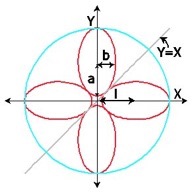
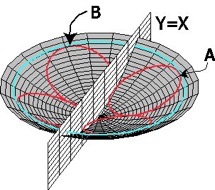
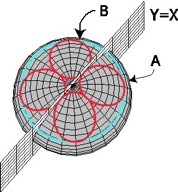
Spherical Flower Problem Euclidean Flower Problem Hyperbolic Flower Problem
One of my students won an award for her presentation on this at MathFest in Providence, Rhode Island.
Generalized Area Principle
Summer 2003
I worked with one student over this summer. We extended the Area Principle to spherical and hyperbolic geometry. The Area Principle states that for the configuration below, in the Euclidean plane, that the ratio of the area of the triangle A1BC over the area of triangle A2BC is the same as the ratio of length A1P over the length of A2P.
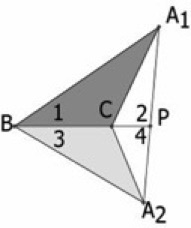
During the first part of the summer we extended this to spherical geometry. During the second part of the summer we extended it to hyperbolic geometry. We used the upper half sheet of the hyperboloid of two sheets to model hyperbolic geometry, where triangles look like:
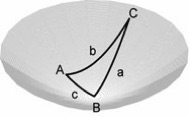
The manuscript containing our results was published in Mathematics Magazine in October 2006 . This student won an award for her presentation at MathFest in Boulder, Colorado.
Spherical Trilateral Theorems
Summer 2002
I worked with a student on extending the triangle theorems (e.g. SAS, SSS, SAA, ASA, SSA, AAA) from the Euclidean plane to a larger class of ‘triangle’ like figures on the sphere. For example the following are pictures of some of the more interesting trilaterals on the sphere:
Basket Trilateral
Witch Hat Trilateral
Trefoil Trilateral
Bowtie Trilateral
Spoon Trilateral
Small Trilateral