> with(plots):with(linalg):with(plottools):

The Polya vector field F of a function f(z)=f(x+iy)=u(x,y)+i*v(x,y) is defined to be the set of vectors

F=[F_x,F_y]=[u(x,y),-v(x,y)] in the plane. Here F_x, and F_y, denote the x and y components of

the vector field. (They do not represent partial derivatives.) In the theory of electricity

and magnetism, one can think of the Polya vector field as either

an electrostatic field F or a magnetic field B.

Below is the Polya vector field corresponding to f(z)=1/z. Note the behavior of the field at the

singularity z=0. In physics, the singularity at z=0 represents a point charge.

> f:=z->z^2;

> u:=unapply(evalc(Re(f(x+I*y))),(x,y));

> v:=unapply(evalc(Im(f(x+I*y))),(x,y));

> F:=[u(x,y),-v(x,y)];

> g1:=fieldplot(F,x=-1..1,y=-1..1,arrows=thick,color=red,grid=[5,5]):display(g1);

> g := transform((x,y) -> [2*x,y]):
display({g(g1)});

1. Where are the arrows largest in length? Where are they smallest in length. Through how many

revolutions do the arrows rotate as one travels a path around the origin?

2. Repeat the above question using f(z)=z^2 and then f(z)=z^3.

The DEL operator is defined to be the partial derivative operator

+ + .

The divergence of a vector field F = [F_x, F_y] at a point is defined to be the

scalar quantity obtained by taking the dot product of DEL with the value of the

vector F at that point. In other words,

div(F) = +

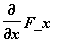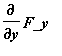
Intuitively, the divergence measures net inflow/outflow of

the vector field at that point.

3. Show that if f is differentiable at a point z=z0, then the divergence of the corresponding

Polya vector field is zero there. (Hint: Use the dot product, together with the Cauchy-Riemann equations.)

Below Maple calculates the divergence for the Polya field above.

> diverge([op(F),0], [x,y,z]);

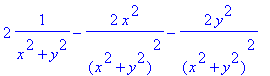
The curl of a vector field F = [F_x, F_y] at a point is defined to be the

vector quantity obtained by taking cross product of the DEL operator

with the vector F_z*i + F_y*j + F_z*k at that point.

Intuitively, the curl measures rotational tendency of the vector field at that

point. Think of placing a paddle wheel placed at a point with its blade perpendicular

to the plane. If the paddle wheel rotates, the curl is different from zero.

4. Show that if f is differentiable at a point z=z0, then the curl of the corresponding

Polya vector field is zero there. (Hint: Use the cross product, together with the Cauchy-Riemann equations.)

Below Maple calculates the curl for the Polya field above.

> curl([op(F),0], [x,y,z]);

The above results have a significant connection to physics, as the curl and divergence are

essential for formulating the differential form of Maxwell's equations, the four primary

equations that govern the theory electricity and magnetism.