Math as a Bad Penny:
A Modeling Excursion for Exponential Functions
Math & Science Update
17 November 1999
Presenters: Dr. Esther Billings & Dr. John Golden
Grand Valley State University
Mathematics & Statistics Department
616-895-2040
billinge@gvsu.edu
goldenj@gvsu.edu
| Penny Experiment | Paper Folding |
Directions for Penny Experiment:
|
Toss # |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
# of Terminated Pennies |
1. Make a bar graph of the relationship between toss number and number of pennies terminated.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| List 3 patterns do you notice in the table. | List 3 patterns you notice in the graph. |
| a. | a. |
| b. | b. |
| c. | c. |
3. What kind of function does this appear to be? Why?
4. Using the data that you gathered, determine a "best fit" equation that could model the data you collected. Describe the process you used to determine this equation. 5. Determine a function which best fits what theoretically should happen. What role does the probability of a coin coming up heads play in your function? 6. This experiment can be run using many other manipulatives than pennies: dice, thumbtacks, M&M's or skittles,… even little plastic pigs as found in pig mania. This can add an interesting feature of non-even probabilities or unknown probabilities. Imagine that, instead of a penny, we used dice that terminated on rolling a six. If we begin with 100 dice, generate a table of how many dice should terminate vs. the roll number.
|
Roll # |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
# of Terminated Dice |
7. Often exponential patterns are recognized by finding a common ratio between one data point and the next. Calculate the ratios between your data points above. Are they what you expected? How can you account for the value of your ratios?
|
Toss #s |
2/1 |
3/2 |
4/3 |
5/4 |
6/5 |
7/6 |
8/7 |
9/8 |
10/9 |
11/10 |
12/111 |
|
Ratio of Terminated Pennies |
8. Determine a best-fit function for table in (6). What role does the probability of a die terminating play in your function?
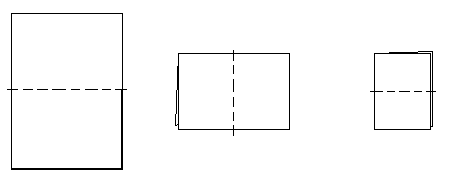
Paper Folding
Materials: Any size piece of paper.
One way to generate exponential patterns for your students to explore is through repeated folding of a piece of paper. One thing to know beforehand is the maximum number of times one can fold a piece of paper in half. Experiment to find out.
1. How many times can it be folded? Is it different depending on the size of the paper?

2. Unfold the paper. Brainstorm with your groupmates about exponential patterns your students could look for in this piece of paper. Consider variables such as number of folds, number of rectangles, area, etc.
3. Choose one of the patterns your group determined. Express the pattern as a table and as a symbolic rule.
4. Is it possible to fold the paper differently to bring out other exponential patterns? What different folding techniques or patterns can you imagine?