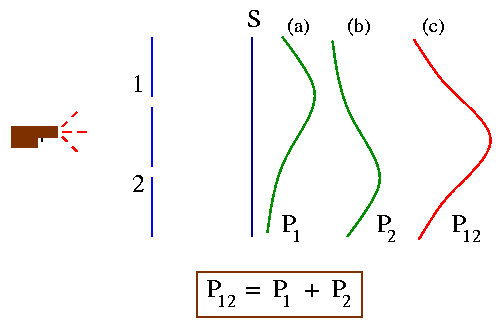
| Wave - Particle Duality |
We have seen that Compton effect is a direct evidence of the corpuscular nature of light. On the other hand the phenomena of interference, diffraction, and polarization reveal the wave nature of light. Louis de Broglie proposed that this dual character of light may also be a characteristic of the subatomic particles like electrons. According to Broglie's proposal a material particle of energy E and momentum p may exhibit characteristics of waves of wavelength l as
l= h/p, Eq. (1)
where h is the Planck's constant and its frequency is determined by Planck's energy quantization expression:
E = hf. Eq. (2)
Eqs. (1) and (2) can be rewritten as follows,
p = h/l = hbar k, E = hbar w, Eq. (3)
where k=2p/l is the wavenumber and w=2pf is the circular frequency.
The dual nature of matter (wave or particle) is hard to digest. To understand this we do a series of thought experiments with 'bullets' and 'electron guns' as proposed by the famous physicist R. P. Feynman [Examples taken from Feynman Lectures in Physics - Volume III].
First Thought Experiment with Indestructible Bullets:
Our experimental setup is shown in the figure below. We also have machine gun (not AK 47!) that shoots a stream of bullets. In front of the machine gun we have a wall with two holes which are big enough for the bullets to pass through. Beyond the wall we have a screen which will absorb the bullets when they hit it. We then can count the number of bullets that have passed through the wall and have been absorbed in the screen.
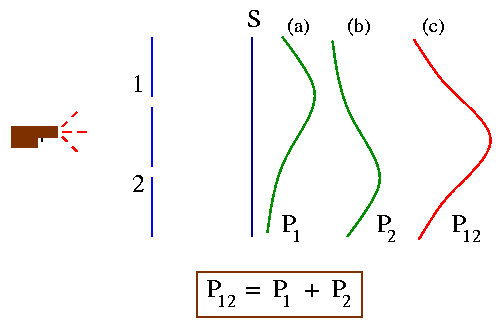
We may now ask the following question
"What is the probability that a bullet can be found on the screen at a distance 'x' (from the center of the screen) after it made its trip through the holes?"
The result of such an experiment is plotted in the graph in Fig. (c) above. We call the probability P12 as the bullets can come through any of the holes 1 and 2.
Now we do the same experiment but we close one of the hole, say hole 2. The probability of the bullets to pass through hole 1 and hit the screen is say P1 [Fig (a) above ] .
Similarly we close hole 1 and let the bullets pass only through hole 2 - say the probability distribution in this case is P2 [Fig. (b)]. Comparing parts (b) and (c) of the Fig. above we find the important result that:
P12 = P1 + P2.
The probabilities just add together. Thus we can say that the effect of both holes open is the sum of the effects with each hole open alone. The important observation in this example is that there is 'no interference.'
Young's Double-Slit Experiment:
A parallel beam of monochromatic light is incident on the two parallel slits of width 'a' and separated by a distance 'b'. When both the slits are open we see a interference pattern as you will see in the simulation below. If any one slit is shut off, a single diffraction pattern will be observed.
Please on the simulations below to observe the interference patterns.
A simulation on Young's Double-slit Experiment
Another simulation on the double-slit experiment:
Another simulation on Young's Double-slit Experiment
Yet another simulation on the double-slit experiment:
Second Thought Experiment with Electrons:
We now repeat the same experiment but we have electrons instead of bullets. Instead of machine gun we fire the electron with an electron gun. We have a detector (may be a Geiger counter) which can detect as soon as the electrons hit the screen after passing through the holes. We repeat the same three steps as we did with the bullets:
(1) keep both the holes open - each electron either goes through hole 1 or hole hole 2. The probability in this case say is P12 [Fig. (c) below].
(2) close hole 2 and keep only hole 1 open - each electron have no other choice but will try to go through 1. The probability to find an electron on the screen is P1 [Fig. (a) below].
(3) close hole 1 and keep only hole 2 open - each electron have no other choice but will try to go through 2. The probability to find an electron on the screen now is P2 [Fig. (b) below].
You may think that similar to the case of bullets [Fig. (b) below]
P12 = P1 + P2.
but that's not the case as shown in the graph below!
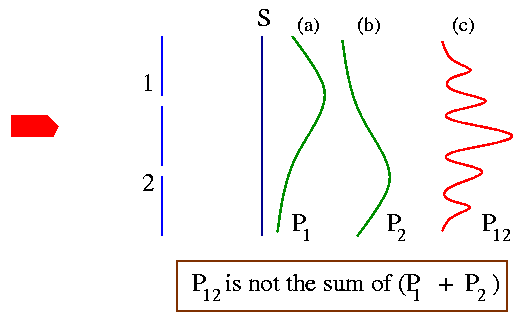
The graphical pattern when both the holes are open are very similar to the interference pattern in the Young's double slit experiment [shown above]. We thus conclude the "There is interference" and we find that, P12 is not just the sum of P1 and P2.
How is it possible?
There is no way you can explain the interference pattern physically if you think electrons as simply particles. Let us first try to understand the mathematics that relates P1 and P2 to P12. We first define the probabilities P1 and P2 in terms of absolute squares of two complex numbers say j1 and j2. We will call j1 and j2 as probability amplitudes. Thus,
P1 = | j1 |2, P2 = | j2 |2.
Remember that P1 gives the effect when hole 1 is open and P2 when hole 2 is open. And the combined effect of two holes is simply
P12 = | j1 + j2 |2.
Now we can see that
P12 = | j1|2 + | j2 |2 + 2| j1| |j2| cosq,
= P1 + P2 + 2 (P1 P2)(1/2) cosq ,
where q is the phase difference between j1 and j2. The last term is the "interference term" and the physics is the same as Young's double slit experiment in optics.
So we conclude with the statement - The electrons arrive in lumps, like particles, and the probability of arrival of these lumps is distributed like the distribution of intensity of a wave. We can then say that an electron behaves "sometimes like a particle and sometimes like a wave."
To see a 'cool' demonostration of this thought experiment (along with understandable text) please on the following link:
Electron Interference Experiment
Third Thought Experiment with Electrons (Watching the electrons!):
To our experiment we add a very strong light source and we place it behind the wall and between the two holes, as shown in the Fig. below. The purpose is to 'watch' the electrons.
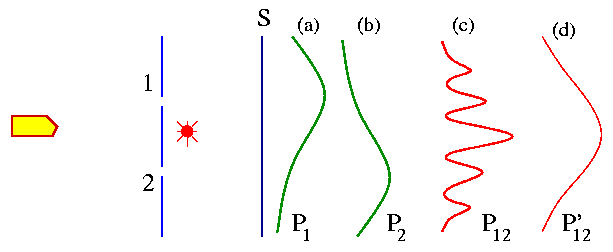
When an electron passes through one of the holes to the detector it will scatter some light to our eyes. We will see a flash of light coming either from the bottom of the light source (if the electron pass through hole 2) or from the top of the light source (if the electron pass through hole 1). We will assume that the electron is an indestructible particle - so we will not see light flashes from the top and the bottom of the light source at the same time. Every time we hear a 'click' from the electron detector we also see a 'flash' either from the top or the bottom of the light source. We repeat the steps in our previous experiments with electrons. Using the light flash we keep count of the electrons that pass through hole 1 or hole 2 and finally make its way to the detector. Say P1 and P2 are the probabilities that electrons reach the detector through hole 1 and hole 2 respectively. After repeating the experiment for many values of x, we get the curves for P1 and P2 as shown in the figure above. What is then the probability that an electron will arrive at the detector by any route? To get that we just have to add the two probabilities i.e. P'12 = P1 + P2. There is no interference [Fig. (d) above]!
We now turn off the light source - the situation is identical to our second thought experiment. In this case we don't look at the electrons as if we don't care about their route to the detector. We are just interested in the results. Now we see interference [Fig. (c) above].
From this experiment we conclude that "when we look at the electrons the distribution of them on the screen is different than when we do not look." In other words, if the electrons are not seen, we have interference.
In our experiment we find that it is impossible to arrange the light in such a way that one can tell which hole the electron went through, and at the same time not disturb the interference pattern. This is a general consequence of Heisenberg's uncertainty principle which we will discuss later.
We now briefly summarize our results.
The probability of an event in an ideal experiment is given by the square of the absolute value of a complex number j which is called the probability amplitude:
P = probability,
j = probability amplitude,
P = | j |2.
When an event occur in several alternative ways, the probability amplitude for the event is the sum of the probability amplitudes for each way separately. There is interference:
j = j1 + j2 ,
P = | j1 + j2 |2.
If an experiment is performed which is capable of determining whether one or another alternative is actually taken, the probability of the event is the sum of the probabilities for each alternative. The interference is lost:
P = P1 + P2.
The Uncertainty Principle:
Considering the experimental limitations of experiments Heisenberg proposed his famous uncertainty principle which is the basis of quantum mechanics. If you make a mesurement on any object and you measure the x-component of its momentum with an uncertainty Dpx (please read delta px), then you can not at the same time, know its x-position more accurately than
Dx = h/Dpx,
where h is the Planck's constant.
The uncertainties in the position and momentum of a particle at any instant must have their product greater than Planck's constant. Mathematically,
Dx Dpx >= h
This realtion is known as Heisenberg's uncertainty principle. The above one-dimensional consideration can be extended to 3-dimesnions.
Dx Dpx >= h, Dy Dpy >= h, Dz Dpz >= h.
The uncertainty principle can also be expressed in other forms. If E is the energy of a quantum system at the time t, then the uncertainties DE and Dt are related by the equation
DE Dt >= h.
Heisenberg's Gamma Ray Microscope:
To examine the uncertainty principle of Heisenberg, N. Bohr proposed this hypothetical experiment which consists of a gamma ray microscope as shown below.
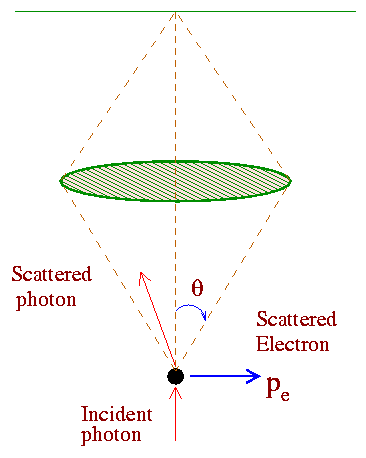
The idea is to detect an electron as exactly as possible. To do that Bohr assumed that very short wavelength radiation (gamma rays) may be used to 'illuminate' the electron and this radiation scattered from the electron may then be observed by means of the gamma-ray microscope. Since ordinary optical parts can not focus gamma-rays, such an experiment is actually hypothetical.
Now according to physical optics, the smallest distance Dx between two points in an object that will produce separated images in a microscope is given by (this is known as the resolving power of a microscope),
Dx = l/2sinq, Eq. (4)
where 2q is the angle subtended by the objective lens as shown in the figure. Now gamma rays of energy hf, possess momentum p = hf/c= h/l. We assume that the scattered gamma-ray to have the same momentum p which it has originally when it enters the microscope. To be collected by the lens, the photon may be scattered through any angle between -q to +q. This imparts to the electron an x- component of the momentum px having any value between + h sinq/l to -h sinq/l. Thus the uncertainty in the electron's momentum is,
Dpx = 2h sinq/l. Eq. (5)
Multiplying Eqs. (4) and (5) we get,
Dpx Dx = h.
This is in agreement with the uncertainty principle.
Group and Phase velocity:
According to de Broglie a particle (or matter) of energy E and momentum p also possess charactersitics of waves of wavelength l [Eq. (3) above]. Now classically a wave of definite wavelength and frequency is of infinite extent in space and is of infinite duration. On the other hand a particle is localized at a definite point in space at a given instant of time (with a definite momentum and energy). Thus the two pictures (wave and particle) are incompatible. What we need is a "wave group" or pulse which is localized in a finite region of space. This is shown in the Fig. below.
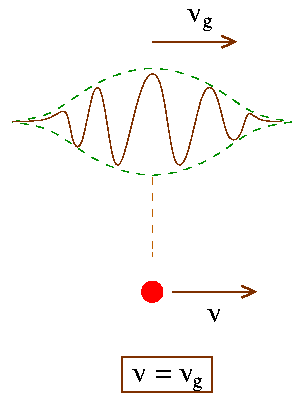
To obtain such a localized wave group (or wave packet) we need to superpose waves of different wavelengths upon one another. Let us examine the situation mathematically:
Consider a one-dimensional wave of wavelength l and frequency f propagating in the +x direction with a phase velocity vp (the crest and trough of the wave moves with this velocity). Such a wave can be mathematically described as:
y = A cos( 2px/l - 2pft),
where A is the amplitude of the wave and y is the displacement along the +y axis. We can rewrite the same equation in a slightly different fashion as:
y = A cos( kx - wt ),
where, k = (2p/l) is the wave-number and w = (2pf ) is the circular frequency. The phase velocity of the wave is given by, w/k = 2 p f l/(2p) = f l = vp. Thus we have the phase velocity in terms of the frequency w and wave number k as,
vp= w/k.
Now imagine two such moving waves of slightly different wave numbers k1 and k2 and with slightly different frequencies w1 and w2.
y1 = A cos(k1x - w1t), y2 = Acos(k2x - w2t).
Using the principle of superposition the resultant wave is,
y = y1 + y2 = A[ cos(k1x - w1t)+cos(k2x - w2t) ]. Eq. (6)
We now use an identity from trigonometry:
cosB + cosC = 2 cos [(B-C)/2]cos [(B+C)/2].
Eq. (6) now becomes
y = A' cos [(k1+k2)x/2 - (w1+w2)t/2 ], Eq. (7)
where
A' = 2A cos[(k1-k2)x/2 - (w1-w2)t/2 ]
= 2A cos [ (Dk/2) x - (Dw/2) t]. Eq. (8)
and D k = |k1-k2|, Dw =|w1-w2| in the above expression. From Eq. (8) we see that the amplitude is no more a constant - rather it depends on both the position and time. We can interpret this as a broad oscillating envelope or wave group or wave packet which moves at a velocity
vg = Dw/Dk = dw/dk (in the limit Dk -> 0). Eq. (9)
vg is known as the group velocity. The phase velocity can be calculated from Eq. (7) which is
vp = (w1 + w2)/(k1 + k2). Eq. (10)
For two waves with nearby frequencies, w1 and w2 are approximately the same and also the wave numbers k1 and k2. In that case we can approximate Eq. (10) as,
vp = w/k. Eq. (11)
Thus the high-frequency wave moves at the phase velocity vp. Using Eqs. (9) and (11) we get a relationship between the group and phase velocities.
vg = dw/dk = d(k vp)/dk = vp + k dvp/dk. Eq. (12)
Eq. (12) can be rewritten in terms of the wavelength l
vg= vp - l (dvp/dl). Eq. (13)
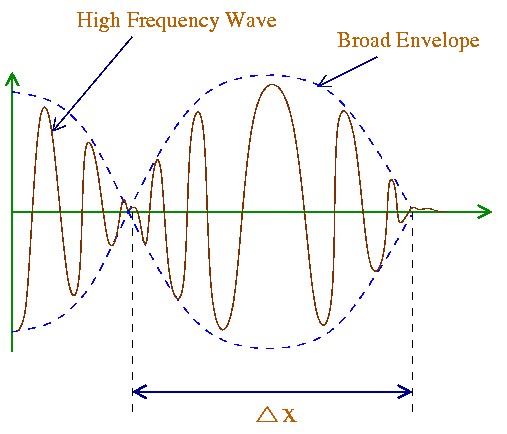
The phase velocity in general depends on the wavelength l. Materials in which the phase velocity varies with wavelength are said to exhibit dispersion (example the different colors of light travel at different speed inside a glass which is a dispersive medium). For light waves in vacuum, there is no dispersion. So dvp/dl= 0 and thus vg= vp= c.
To see a nice demonostration of the group and the phase velocities of a wave please on the simulation below:
A simulation on Group and Phase velocities of a travelling wave
From Eq. (8) we can see that the envelope term A'=2A cos[(Dk/2)x] (at t=0) has minima (which means A'=0) when (Dk/2) x = (n+1/2)p where n=0,1,2,.... The distance between two successive minima Dx satisfies the condition,
(Dk/2) Dx = p => Dk Dx = 2p. Eq. (14)
Recall that Dk = |k1 - k2| is the range of wavenumbers present. Similarly, if x is held constant (say x = 0 ) and time t is allowed to vary in the envelope portion, the result we get is (Dw/2)Dt=p or
Dw Dt = 2p. Eq. (15)
A general characteristic of wave groups is that they are both of limited spatial diatnce Dx and limited time duration Dt. The smaller the spatial width of the pulse, Dx, the larger the range of wavelengths (or wavenumbers), Dk, needed to form a pulse. Mathematically this mean
Dk Dx = 1. Eq. (16)
Similarly if the time duration, Dt, of the pulse is small, we need a wide spread of frequencies, Dw, to form the group. Mathematically,
Dt Dw = 1. Eq. (17)
In electronics, this condition is known as the "response time-bandwidth formula." The above expression shows that in order to amplify a voltage pulse of time width Dt without distortion, a pulse amplifier must equally amplify all frequencies in a frequency band of width Dw.
We will now do an example to show how to calculate the group and the phase velocities.
An Example:
Phase and Group velocities of de Broglie waves -
The phase velocity of the de Broglie waves is,
vp = f l = w/k.
Now from the special theory of relativity, we have for the electrons the total energy E and the momentum p as (m0 is the rest mass or the proper mass)
E = gm0 c2 = hbar w, p = gm0 v = hbar k,
where g = 1/[1-v2/c2]½ is the Lorentz factor. Thus we have,
E/p = c2/v = w/k.
The phase velocity is then, vp = w/k = c2/v, where v is the velocity of the electrons and c is the velocity of light in vacuum. According to de Broglie's hypothesis, v = vg, the group velocity of the de Broglie waves. Hence we have a relationship between the group and the phase velocities of the de Broglie waves,
vp = c2/vg => vp vg = c2.
On the other hand, the phase velocity can be obtained from the relativistic expression for the energy
E2 = p2c2 + m02c4 => hbar2 w2 = hbar2 c2 k2 + m02c4.
Substituing w = vpk, and solving for vp in the above expression yields,
vp = c [1 + (m0 c/hbar k)2]½ = c [ 1+ (m0 c l/h)2]½ .
Thus we have an expression for the phase velocity of the de Broglie waves. We can clearly see that vp > c - but we know from the postulates of special relativity that nothing (no information) can travel faster than the speed of light 'c' in vacuum. Then what's wrong? Before we answer the question let us calculate the group velocity which is
vg = c2/vp = c/[1+ (m0 c l/h)2]½ < c.
The answer to the puzzle is that information is only carried by the wave group that moves with a group velocity vg (not by the individual frequencies which move with a phase velocity vp that can be larger than the speed of light). And the group velocity is always less than c - thus our quantum mechanics is consistent with special relativity. As an example, the propagation of radio waves, signals are transmitted after modulation, either of the amplitude or of the frequency. Production of amplitude modulated signals involves the superposition of many plane waves of different frequencies, centered about a mean frequency. The energy carried by such modulated signals is transmitted with the group velocity not by the phase velocity of the component waves.
Reference:
© Kingshuk Majumdar (2000)