In Part I we studied the Hydrogen atom, learned about the different quantum numbers. In Part II we will study the effect of magnetic field on the energy levels (as an example say of the hydrogen atom). We will learn about a new quantum number - the 'spin' quantum number. Finally we will study the rules governing the electronic configurations of the elements in the periodic table. 

In Part I we found that the acceptable wavefunctions of the hydrogen atom can be found only if the energy E is restricted to be one of the following special values:

E_n = -(me⁴/2hbar²)(Z²/n²),    n=1,2,3,....

Note that the allowed energies depend only on the principal quantum number n. Keeping n fixed but allowing l [l can vary from 0 to (n-1)] and m_l [m_l varies from -l,-(l-1),...,0,...(l-1),l] to vary the energy doesnot change. This is another example of degeneracy. States with fixed n have same energies for different l and m_l. But this degeneracy can be partially removed by applying an external magnetic field. This is known as the Zeeman effect.

Orbital Magnetism And The Zeeman Effect :

It is known from classical electromagnetic theory (Maxwell's equations)  that a rotating charged body gives rise to a magnetic field. So an electron orbiting the nucleus of an atom generates a magnetic field. The atom thus behaves like a tiny magnet with magnetic moment m. It can be easily shown that for a circulating charge (of charge q and mass m) the magnetic moment m is proportional to the orbital angular momentum L. Moreover, m and L are in the same direction. Mathematically,

m = (q/2m) L.

The constant (q/2m) is called the gyromagnetic ratio. For the case of an electron rotating around the nuclues the magnetic moment is in opposite direction to the angular momentum as the charge of the electron is negative. So in case of electrons we have,

m = (-e/2m_e) L.

Considering only the z-component we get,

m_z = (-e/2m_e) L_z = -(e hbar/2m_e) m_l = -m_B m_l,     (As L_z = m_l hbar)

where, m_B = e hbar/2m_e = 9.274 x 10^-24 J/T is called the Bohr magneton. It is a natural unit for the atomic moment. Thus we can see that m_z can take only special values.

The interaction of an atom with an applied magnetic field depends ont he size and orientation of the atom's magnetic moment. With the application of a magnetic field B, the atom experiences a torque t,

t = m x B.

If the applied magnetic field is in the z-direction the atom precesses around the field direction with a frequency w_L known as the Larmor frequency,

w_L = (e/2m_e) B.

It can be shown from electromagnetic theory that the energy of a magnetic dipole in an external magnetic field B is,

U = -m.B = (e/2m_e) L.B = (eB/2m_e)L_z = hbar w_L m_l.

Equation above shows that the magnetic energy of an atomic electron depends on the magnetic quantum number m_l and hence, is quantized. The total energy of this electron is the magnetic energy U plus the energy it had in the absence of an applied field (E₀). So we have,

E = E₀ + hbar w_L m_l.

For atomic hydrogen, E₀ depends only on the principal quantum number n. We can see that in presence of the magnetic field the energy levels are no longer degenerate. For example, for the first excited state n=2, l=1, m_l can take three values -1, 0, and 1. Thus the energies are

E₁ = E₀ - hbar w_L,      E₂ = E₀, and   E₃ = E₀ + hbar w_L.

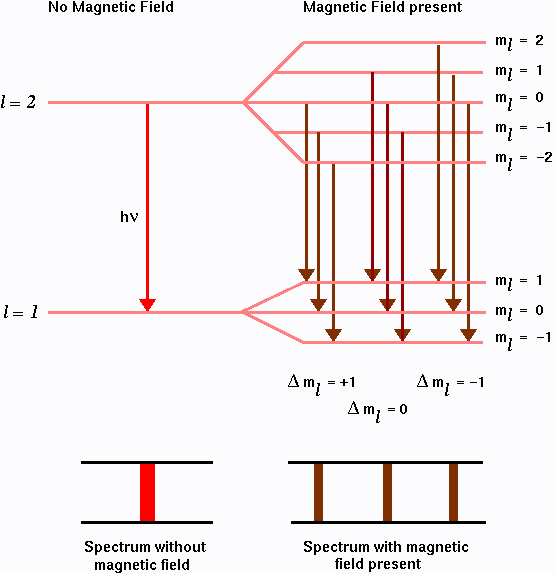
So the single line will split in to three equally spaced lines (thus partially lifting the degeneracy) as shown in the figure below:

The splitting of energy levels in presence of magnetic field is known as the Zeeman effect. Zeeman spectral lines and the underlying atomic transition that give rise to them for an electron follows from the selection rules discussed before (Part I). The allowed atomic transitions from l=2 to l=1 level are shown in the figure above.

Finally, even the splitting of an emission line into a triplet of equally spaced lines as predicted, which is called the normal Zeeman effect is not observed experimentally. In the experiment one observes for than three spectral lines (four, six or even more). This is the anomalous Zeeman effect which is due to the existence of the electron spin (to be discussed below).  

Electron Spin:

Electrons (in general any quantum particle) not only possess magnetic moment due to orbital motion but also possess magnetic moment due to spin. The spin magnetic moment for a charged particle (of charge q) is,

m_s = g (q/2m) S.

g is called is the Lande g-factor. For electrons it can be shown from relativistic quantum mechanics that the value of g is slightly greater than 2.  So the total magnetic moment is the sum of the orbital and spin moments:

m = m_l + m_s = (q/2m) [ L + g S]

For electrons, it is

m = m_l + m_s = (-e/2m) [ L + g S]

The existence of a spin moment of the electron was first demonostrated in a classic experiment by O. Stern and W. Gerlach. In their experiment, a beam of neutral silver atoms was passed through a non-uniform magnetic field (created between the poles of a larger magnet - see figure below). The beam was detected by being deposited on a glass collector plate. 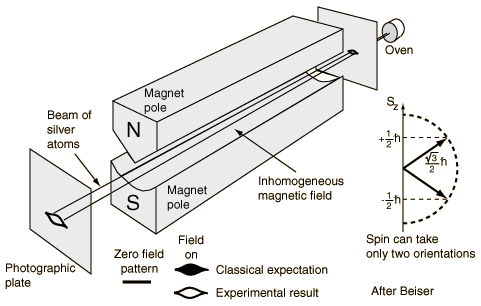A non-uniform magnetic field exerts a force on any magnetic moment, so that each atom is deflected in the gap by an amount governed by the orientation of its moment with respect to the direction of inhomogeneity (the z axis). Thus, the atomic beam should split into a number of discrete components, one for each distinct moment orientation present in the beam. In the Stern-Gerlach experiment, it was observed that the silver atomic beam was clearly split into two components. On the other hand the silver atoms in their ground state have zero angular momentum (l=0) as outermost electron is in the s-state. The splitting of the beam in two cannot be explained from the space quantization where one would predict the beam to split in 2l+1 = 1 component. To explain this, we have to introduce the concept of spin and the spin quantum number m_s.

|S| = [(s(s+1)]^1/2 hbar = 3^1/2/2 hbar,   

      m_s = +1/2 refers to the up spin case and m_s = -1/2 refers to the spin down case.

Stern-Gerlach experiment for l=1 electrons are shown below -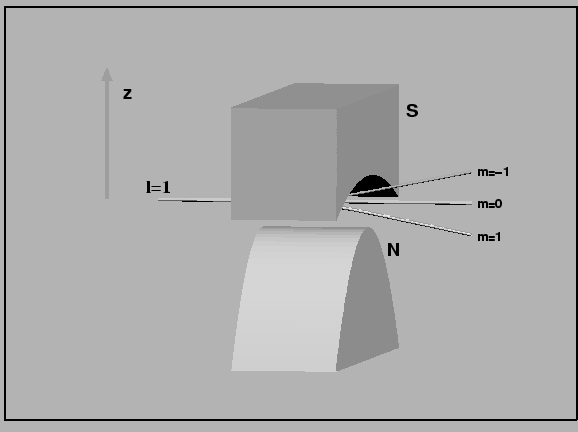

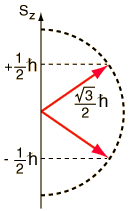
The spin angular momentum also exhibits space quantization. The figure below shows the two allowed orientations of the spin vector S for a spin 1/2 particle (e.g. electron):

Total Angular Momentum:

The electron thus have both orbital (L) and spin angular momentum (S). The existence of both orbital and spin moments for the electrons lead to their mutual interaction known as the spin-orbit interaction. The coupling of spin and orbital moments implies that neither L or S is conserved separetly. But the total angular momentum (J) which is just the sum of L and S i.e. J = L + S is conserved. Thus |J| and |J_z| are quantized and only takes the following values:

|J| = [j(j+1)]^1/2 hbar,     J_z = m_j hbar with    m_j = j, j-1,...., -j.

Permissible values for the total angular quantum number j are

j = l+s, l+s-1, l+s-2, ....,|l-s|.

The existence of spin requires that the state of an atomic electron has to be specified with four quantum numbers l, s, m_l, and m_s. If the spin-orbit interaction is taken into account, m_l and m_s are replaced by j and m_j. In either case four quantum numbers are required, one for each of the four degrees of freedom possessed by a single electron.

Consider a system where two or more electrons are present. It is natural to ask "How many electrons in an atom can have the same four quantum numbers in the same state?" According to Pauli "no two electrons in an atom can have the same set of quantum numbers." This is the famous Pauli's exclusion principle. The exclusion principle follows from tha fact that the electrons are identical particles - it is not possible to distinguish between two electrons. 

Exchange Symmetry

Let us consider the two-particle wavefunction Y(r₁, r₂) which depends on both the particles 1 (at position r₁) and 2 (at position r₂). |Y(r₁, r₂)|² then represents the probability density for finding one electron at r₁ and the other electron at r₂. Now if the particles are indistinguishable a formal interchange of particles produce no observable effects. Mathematically,

|Y(r₁, r₂)| = |Y(r₂, r₁)|

Such a wavefunction then said to have a exchange symmetry. But the wavefunction itself may be either even or odd under exchange symmetry i.e. we can have two following cases:

Y(r₁, r₂) = + Y(r₂, r₁)  (Bosons)

Y(r₁, r₂) = - Y(r₂, r₁)  (Fermions)

The particles with even exchange symmetry are known as bosons (we will see later that they obey Bose-Einstein statistics). Photons (quanta of electromagnetic wave), phonons (quanta of lattice vibrations), pions  etc. are examples of bosons. Bosons have integer spins.

The particles with odd exchange symmetry are known as fermions (they obey Fermi-Dirac statistics). Electrons, protons, neutrinos, etc  are examples of fermions. Fermions have half-integer spins.

Electron Configurations & The Periodic Table:

The Relative Energies of Atomic Orbitals

Because of the force of attraction between objects of opposite charge, the most important factor influencing the energy of an orbital is its size and therefore the value of the principal quantum number, n. For an atom that contains only one electron, there is no difference between the energies of the different subshells within a shell. The 3s, 3p, and 3d orbitals, for example, have the same energy in a hydrogen atom. The Bohr model, which specified the energies of orbits in terms of nothing more than the distance between the electron and the nucleus, therefore works for this atom. The hydrogen atom is unusual, however. As soon as an atom contains more than one electron, the different subshells no longer have the same energy. Within a given shell, the s orbitals always have the lowest energy. The energy of the subshells gradually becomes larger as the value of the angular quantum number becomes larger.

Relative energies: s < p < d < f

A very simple device can be constructed to estimate the relative energies of atomic orbitals. The allowed combinations of the n and l quantum numbers are organized in a table, as shown in the figure below and arrows are drawn at 45 degree angles pointing toward the bottom left corner of the table.

The order of increasing energy of the orbitals is then read off by following these arrows, starting at the top of the first line and then proceeding on to the second, third, fourth lines, and so on. This diagram predicts the following order of increasing energy for atomic orbitals.

1s < 2s < 2p < 3s < 3p <4s < 3d <4p < 5s < 4d < 5p < 6s < 4f < 5d < 6p < 7s < 5f < 6d

< 7p < 8s ...

The electron configuration of an atom describes the orbitals occupied by electrons on the atom. The basis of this prediction is a rule known as the aufbau principle, which assumes that electrons are added to an atom, one at a time, starting with the lowest energy orbital, until all of the electrons have been placed in an appropriate orbital. A hydrogen atom (Z = 1) has only one electron, which goes into the lowest energy orbital, the 1s orbital. This is indicated by writing a superscript "1" after the symbol for the orbital.

H (Z = 1): 1s¹

He (Z = 2): 1s²

The third electron goes into the next orbital in the energy diagram, the 2s orbital.

Li (Z = 3): 1s² 2s¹

Be (Z = 4): 1s² 2s²

After the 1s and 2s orbitals have been filled, the next lowest energy orbitals are the three 2p orbitals. The fifth electron therefore goes into one of these orbitals.

B (Z = 5): 1s² 2s² 2p¹

C (Z = 6): 1s² 2s² 2p²

However, there are three orbitals in the 2p subshell. Does the second electron go into the same orbital as the first, or does it go into one of the other orbitals in this subshell? To answer this, we need to understand the concept of degenerate orbitals. By definition, orbitals are degenerate when they have the same energy. The energy of an orbital depends on both its size and its shape because the electron spends more of its time further from the nucleus of the atom as the orbital becomes larger or the shape becomes more complex. In an isolated atom, however, the energy of an orbital doesn't depend on the direction in which it points in space. Orbitals that differ only in their orientation in space, such as the 2p_x, 2p_y, and 2p_z orbitals, are therefore degenerate. Electrons fill degenerate orbitals according to rules first stated by Friedrich Hund. Hund's rules can be summarized as follows. One electron is added to each of the degenerate orbitals in a subshell before two electrons are added to any orbital in the subshell. Electrons are added to a subshell with the same value of the spin quantum number until each orbital in the subshell has at least one electron.When the time comes to place two electrons into the 2p subshell we put one electron into each of two of these orbitals (The choice between the 2p_x, 2p_y, and 2p_z orbitals is purely arbitrary).

C (Z = 6): 1s² 2s² 2p_x¹ 2p_y¹

The fact that both of the electrons in the 2p subshell have the same spin quantum number can be shown by representing an electron for which s = +1/2 with an arrow pointing up and an electron for which s = -1/2 with an arrow pointing down. The electrons in the 2p orbitals on carbon can therefore be represented as follows.

When we get to N (Z = 7), we have to put one electron into each of the three degenerate 2p orbitals.