GVSU REU

SUMMER 2019

THE HAUSDORFF METRIC GEOMETRY AND GRAPH THEORY

Steven Schlicker

My Background

I started conducting research with undergraduate students in 1990 with a project involving fractal geometry and regular polygons. I continued this type of research when I came to Grand Valley, ultimately deciding to apply to the National Science Foundation to form a Research Experiences for Undergraduates (REU) site at GVSU. We hosted our first REU site in 1999 and our program has been running strong ever since. My current interests are in the geometry the Hausdorff metric imposes on the space of compact sets, and I have been engaged in this area since 2001. My groups have published several papers (listed in the references) and presented their work at local, regional, and national conferences. The sections below provide a bit of information about this project for summer 2019, and I look forward to continuing this research.

A Polygonal Chain Graph that Generated Previously Unknown Integer Sequences.

What Will This Research Involve?

I study the geometry of the Hausdorff metric. You are probably familiar with standard Euclidean geometry where we study relationships between points, lines, and line segments. The geometry we will explore in this summer REU is quite different – the “points” are objects (like your coffee cup or I-Phone) and the Hausdorff metric provides a way for us to measure the distance between these objects. This distance then imposes a geometry on the space of objects, and it is consequences of that geometry that we will study.

We have learned a lot about this geometry in past REUs. For example, we have completely classified circles in this geometry, have made connections to number theory (including discovering an infinite three-parameter family of integer sequences – connected to the figure at the top of this page), found that lines in this geometry can just stop, and proved fascinating facts about the primes 19 and 37. Most recently, we have been investigating the concept of Pythagorean orthogonality in this space.

Project for Summer 2019

In the paper Polygonal chain sequences in the space of compact sets, two REU students and I created an infinite three parameter family of previously unknown integer sequences. These sequences are determined by the number of points that line at each location on a line segment between two types of sets, called configurations. An example of a configuration is the two sets (one consisting of red points and the other the blue points) in the figure at the top of this page. (Unlike in Euclidean geometry, there can be many different points at the same location on a line segment.) The configurations we constructed were called polygonal chains, and one such chain is shown at the top of this page. This work resulted in the paper mentioned as well as with several entries (A152927, A152928, A152929, A152930, A152931, A152932, A152933, A152934, A152939) in the On-Line Encyclopedia of Integer Sequences.

This summer I hope to connect the ideas in this paper to graph theory. In particular, every finite configuration corresponds to a bipartite graph and every bipartite graph can be considered a finite configuration. With this idea in mind we can assign to each bipartite graph a new number (yet to be given a name), and we can look to discover these numbers for specific families of graphs. One family with which we could begin is the family of complete bipartite graphs, as in the figure below. Time permitting, we could explore other families of bipartite graphs. With any luck, we will discover some more previously unknown integer sequences and discover some interesting patterns.

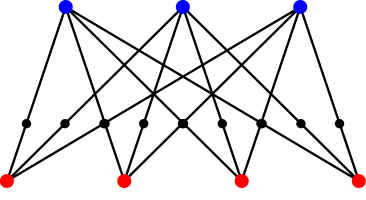
A complete bipartite graph.

Desirable Experiences for Applicants

Applicants should be willing to work collaborative with peers and faculty, but also be capable of independent work. An interest in geometry is important – many of the arguments made in our research involve basic properties of Euclidean lines, segments, angles, and circles – but it is not necessary to have more than a basic familiarity with Euclidean geometry. Some background in writing proofs would be helpful (mathematical induction tends to rear its head in these arguments). Most desirable is a positive attitude toward geometric ideas and the willingness to just muck around with sets.

What This Project Is Not

Although the Hausdorff metric has many real life applications, I know almost nothing about them and they are not related to this research. This is a project in PURE MATHEMATICS.

How To Apply

For application information and instructions, please visit the GVSU Summer Mathematics REU home page.

References

· Pythagorean Orthogonality of Compact Sets, with Pallavi Aggarwal* and Ryan Swartzentruber*. Involve, a Journal of Mathematics, 11-5 (2018), 735--752. DOI 10.2140/involve.2018.11.735.

· Missing edge coverings of bipartite graphs and the geometry of the Hausdorff metric, Katrina Honigs*. Journal of Geometry, April 2013, Volume 104, Issue 1, 107-125.

· A Missing Prime Configuration in the Hausdorff Metric Geometry, Chantel Blackburn*, Kristina Lund*, Steven Schlicker, Patrick Sigmon*, and Alex Zupan*. Journal of Geometry, (2009), 92, Numbers 1-2, 28-59.

· Polygonal chain sequences in the space of compact sets, Steven Schlicker, Lisa Morales* and Dan Schultheis*. Journal of Integer Sequences, Vol. 12 (2009), Article 09.1.7.

· Fibonacci sequences in the space of compact sets, Kris Lund*, Steven Schlicker, and Patrick Sigmon*. Involve, Vol. 1 (2008), No. 2, 197-215,

· A Singular Introduction to the Hausdorff Metric Geometry, Dominic Braun*, John Mayberry*, Audrey Malagon*, and Steven Schlicker. Pi Mu Epsilon Journal, Vol. 12, No. 3, p. 129-138, 2005.

· When Lines Go Bad In Hyperspace, Christopher Bay*, Amber Lembcke*, and Steven Schlicker. Demonstratio Mathematica, No. 3, Volume XXXVIII (2005), p. 689-701.

*Denotes an undergraduate author.