The Strange World of the Hausdorff Metric Geometry

XI. Betweenness

Betweenness is a fascinating topic in the geometry of H(Rⁿ) and we have obtained many interesting results related to betweenness. To begin to describe some of the work in the REU program with introduce the next theorem (Lemma 2.5 of [3]) which shows that there may be many elements at a particular location between two given elements A and B in H(Rⁿ).

Theorem 5: Let A, B be distinct elements in H(Rⁿ) with h(A, B) = r. If there exists a in A such that d(a,B) is not equal to r or b in B such that d(b,A) is not equal to r, then there are infinitely many elements C in H(Rⁿ) that satisfy ACB and h(A,C)=s for any 0 <s < r.

In particular, this theorem is more general than the result from [6]. The basic idea is that if a is in A and d(a,B) is not equal to r, then there is a point b in B so that the Euclidean distance from a to b is less than r. Consequently, we can find a point c in ({a})_s ∩ ({b})_t so that for sufficiently small ε the sets M(s) - N_ε(c) lie between A and B at a distance s from A.

As we saw earlier, if A and B are single point sets, then there is exactly one element C in H(Rⁿ) at each location satisfying ACB. So on the one extreme we have exactly one set at a given location between two sets A and B and at the other extreme we have infinitely many sets at a given location between sets A and B. Under certain conditions, given in [3] and summarized in the next theorem, it is possible to have sets A and B so that the number of elements in H(Rⁿ) satisfying ACB at each location between A and B is a finite number (greater than one).

Theorem 6: Let A and B be distinct elements of H(Rⁿ) and let r = h(A, B). If there are finitely many elements C in

H(Rⁿ) satisfying ACB at each location, then

d(a, B) = r = d(b, A)

for every point a in A and every point b in B.

Moreover, in these situations, the number of elements is the same at every location.

As an example, consider the sets A and B consisting of the opposite vertices of a square (shown below with A in red and B in blue). We draw segments connecting points in A and B that are h(A, B) apart. We call such points adjacent points. In Figure 2, the seven different sets of black points each lie between A and B at the same distance from A.

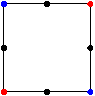
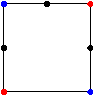
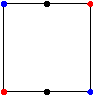
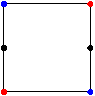
Figure 2

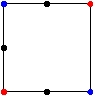
Notice that each of these sets is a subset of the four point set C shown at the far left. In fact, Lemma 3.6 of [6] and Theorem 4 of [7] show that M(s) = (A)_s ∩ (B)_h(A,B)-s is the largest set, in the sense of containment, that lies between A and B at the distance s from A. However, not every subset of M(s) lies between A and B as Figure 3 illustrates.

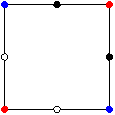
Figure 3

Notice in the example of Figure 3, the left bottom point (in A) is farther than s from the set of black points.

One consequence of this theorem is that if A and B are finite sets satisfying d(a, B) = r = d(b, A) for every a in A and b in B, then there are finitely many elements C in H(Rⁿ) at each location satisfying ACB. Sets A and B that satisfy this condition form what we call a configuration.

Definition: A pair of sets A, B in H(Rⁿ) with h(A, B) = r > 0 form a configuration, denoted [A, B], if d(a, B) = r = d(b, A) for every a in A and b in B.

Theorem 6 shows that if [A, B] is a configuration, then the number of elements between A and B at each location is the same regardless of location. We denote this number by #([A, B]). In our example of A and B as the opposite vertices of a square it is left to the reader to show that the seven sets shown are exactly the sets that are between A and B at a distance s from A and that #([A, B]) = 7 in this case.

In the next section we will look at more examples in which there are finitely many elements at each location between two elements A and B of H(Rⁿ).

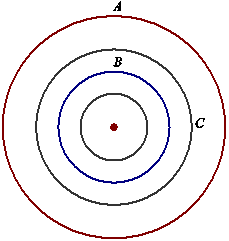
If either A or B is an infinite set, one might think that the situation would be more complicated than in the finite case. In Figures 4, 5, and 6, the set A is the infinite set of points in red, B the infinite set of points in blue, and C the set of points in gray. In each case, C is the largest element, namely (A)_s ∩ (B)_h(A,B)-s, at the indicated location satisfying ACB. In Figure 4, C is the only element at this location satisfying ACB. In Figure 5, we can delete any open arc that is not the entire circle point from the inner of the two circles whose union is C and obtain an element C* in H(Rⁿ) satisfying AC*B at the same location. So in this case, there are infinitely many elements at the indicated location between A and B illustrating the fact that the condition of being a configuration is necessary but not sufficient to ensure a finite number of elements at each location between sets A and B. In Figure 6, we can remove the isolated point from C and obtain an element C* in H(Rⁿ) satisfying AC*B at the same location. So with these infinite sets A and B of H(Rⁿ), we can obtain 1, 2, or infinitely many elements C in H(Rⁿ) satisfying ACB at a given location. However, as we will see later, the infinite case is really no more complicated than the finite case.

Figure 4	Figure 5	Figure 6