The Strange World of the Hausdorff Metric Geometry

XVI. Polygonal Chain Configurations

In 2006, Lisa Morales, Dan Schultheis, and I explored a new family of finite configurations, the polygonal chains. A polygonal chain #(PC_m,l^k) is constructed by chaining together k copies of m polygonal configurations with string configurations of length l. Two examples are shown below.

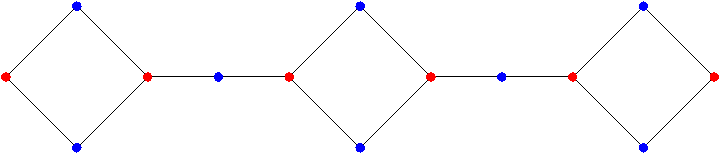
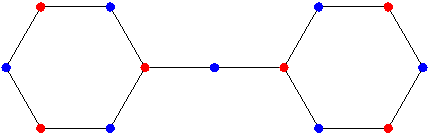
Figure 11

Top: PC_2,2³; Bottom: : PC_3,2²

If we fix two of the parameters k, m, and l and let the other vary, we obtain an infinite sequence of integers #(PC_m,l^k).

For k = 1 we have

#(PC_m,l) = #(P_m) = L_2m and #(PC_m,l+S₁) = #(P_m+S₁) = F_2m+2.

Using a lot of induction and some techniques from linear algebra in [22], we found that for m ≥ 2, k ≥ 2, and l ≥ 1,

#(PC_m,1^k) = R_m,l λ_m,l^k-1 + R_m,l μ_m,l^k-1,

where λ and μ (λ > μ) are the eigenvalues of the matrix M = [m_p,q], with

m_1,1 = L_2mF_l-2 + F_2m+2F_l-1, m_1,2 = L_2mF_l-1 + F_2m+2F_l

m_2,1 = F_2m+2F_l-2 + F_l-1(F_m+2)², m_2,2 = F_2m+2F_l-1 + F_l(F_m+2)²

and

, and .

In these formulas we let F_-1 = 1. The table below shows a few entries in these polygonal chain sequences.

i	1	2	3	4	5
P2^i(S1)	7	113	1815	29153	468263
Pi^2(S1)		113	765	5234	35865
P2^2(Si)	113	176	289	465	754
P2^i(S2)	7	176	4393	109649	2736832
Pi^3(S2)		4393	80361	1425131	25671393
P3^3(Si)	32733	80361	215658	559305	1469565

The polygonal chains provide an infinite three-parameter family of previously unknown integer sequences, some of which can now be found in the On-Line Encyclopedia of Integer Sequences.