| a) bonds | b) bond angles |
|
|
|
| c) dihedral angles | |
|
|
by Mary E. Karpen and Stephanie Schaertel, Grand Valley State University, 8/98
Computational chemistry is a fast growing field within chemistry, which uses computers to help solve chemical problems. Traditionally, computational chemistry refers to a number of computational techniques used to simulate molecular structure and behavior. For example, one can determine the electronic structure of a molecule, calculate the energy required to break a bond, or simulate the motion of water molecules in liquid water. In more recent years, the definition of this field has been broadened to include investigations of molecular structure and behavior through the use of large databases of known chemical structures and behaviors. The properties of a new molecule are then extrapolated from information about similar molecules with known properties. At times, the definition of computational chemistry is so broad that it includes any application of computers to chemistry, for example, in the construction of electronic laboratory notebooks.
In this class, we will focus on the traditional application of computational chemistry - simulating molecular structure and behavior. The American Heritage Dictionary defines "simulate" as "to have or take on the appearance, form, or sound of; imitate"1. This is exactly what we ask the computer to do in computational chemistry - to imitate real molecules. What is the best way to imitate molecules? The best way is to make them as "real" as possible. If you were to simulate a bridge, you would supply the computer with information on the physics of a bridge structure. Simulating molecules is no different - you must supply the computer with the physics of chemistry.
There are generally two types of physics one uses to simulate molecules, Newtonian physics and quantum physics (also called quantum mechanics or quantum chemistry). Modeling methods based on Newtonian physics are called molecular mechanics. Modeling methods based on quantum physics are called ab initio or semi-empirical methods.
The choice of which method you choose to model your molecular system of interest depends on both the size of your system and the nature of your problem. Molecular mechanics calculations take the least amount of computing time for a given number of atoms, semi-empirical methods take a bit more time but are typically more accurate, and the ab initio methods take the longest time but are often most accurate. The table below illustrates the dependence of computing time on the number of atoms in your system:
| Simulation Method |
|
|
|
| Molecular Mechanics |
|
|
|
| Semi-Empirical |
|
|
|
| ab initio |
|
|
|
* These are approximate limits. The actual atom number limit is very dependent on the problem being solved and also on the speed of the computer.
The degree of accuracy required in the simulation will also greatly determine the choice of method; indeed, there are certain events, such as bond breaking, that molecular mechanics simply can not model at any level of accuracy. Molecular mechanics and quantum mechanics methods are briefly described below.
Molecular Mechanics
Molecular mechanics systems are fairly straight-forward
to understand. generally, atom interactions are modeled and bonded interactions
and non-bonded interactions. Letís first look at bonded interactions, which
model behavior of atoms that are covalently bonded together.
Bonded Interactions
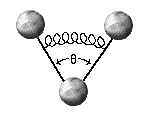
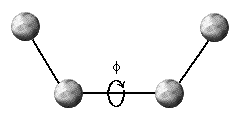
Most molecular mechanics programs model three types of bonded interactions: bond distances, b, bond angles, q, and dihedral angles, f (Fig. 1).
| a) bonds | b) bond angles |
|
|

|
| c) dihedral angles | |

|
|
Bonds are modeled as springs, which can vibrate about an equilibrium position (Fig. 1a). As the spring is compressed, there is a restoring force that pushes the two atoms apart, toward their equilibrium position. Similarly, as the spring is expanded, there is a restoring force pushing the atoms back together toward the equilibrium position. From a potential energy point-of-view, the system has the lowest potential energy when the atoms are at their equilibrium position, and the potential energy increases as the atoms deviate from this position.
Mathematically, we can model this behavior in a computer using the equation
Vb = kb(b-b0)2, (1)
where Vb is the potential energy of the bond, b0 is the equilibrium position, and kb is the spring constant, which determines how stiff the spring is or, equivalently, how strong the restoring force is, forcing the system back to equilibrium. This type of function is called a harmonic potential energy function (Figure 2).
Figure 2: An example harmonic potential energy curve (kb = 1, b0 = 1.5)
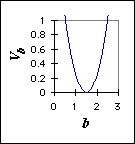
Given that we can model bonds as springs, how do we know what equilibrium distances or the spring constants to choose for these bonds? We could guess, or we could take values from experimental measurements. Of course, we generally choose the latter.
Because of this dependence on experimental data, molecular mechanics is known as an empirical modeling method. Empirical is defined as "relying upon or derived from observation or experiment"1. We will see this term again when discussing quantum mechanical methods.
In Table 2 below, spring constants and equilibrium distances are given for a few example bonds. These two constants are called parameters, in that they are the constants that must be selected to construct the appropriate model.
|
|
|
kb |
|
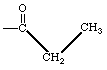
| Bond between a carbonyl carbon and a methyl carbon |
|
|
|
| Bond between a carbonyl carbon and a methylene carbon |
|
|
|
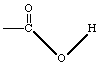
| Bond between a carbonyl carbon and an ester oxygen |
|
|
|
| Bond between a carbonyl carbon and a hydroxyl oxygen |
|
|
* These parameters are taken from the CHARMM force field2.
To model the behavior of bond angles, we again use a spring,
as in Figure 1b, creating another harmonic potential energy function,
Vq = kq(q - q0)2, (2)
where Vq is the potential energy stored in the bond angle, kq is the spring constant, and q0 is the equilibrium angle. Table 3 gives some example parameters for various bond angles. The spring resists openings and closings of the angles from its equilibrium position.
|
|
|
|
 |
|
|
 |
|
|
|
|
|
|
 |
|
|
* These parameters are taken from the CHARMM force field2.
The final bonded interaction we will model are dihedral (also
called torsion) angles (Figure 1c). Unlike bond distances and bond angles, which
show one minimum on their potential energy surface, dihedral angles can have
several minima. That is, these angles often have more than one preferred position.
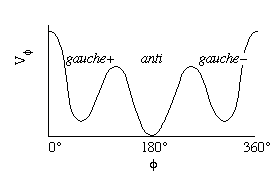
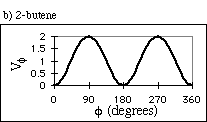
For example, butane has three minima in its potential energy curve, called gauche-,
anti, and gauche+ (Figure 3).
Figure 3: Potential energy surface for butane as a function of the C-C-C-C dihedral angle.
Vf = kf (1 + cos(nf - d)), (3)
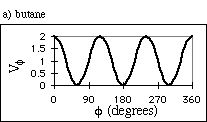
where Vf is the potential energy of the dihedral angle, n is the number of valleys in the potential energy surface, and d is called the "phase", used to shift the curves along the f axis, so the wells are at the appropriate values. For butane, the dihedral angle potential energy has n = 3 and d = 0°. This results in the curve shown in Fig. 4a. For a carbon-carbon double bond, only cis (f = 0°) and trans (f = 180°) are favored. We model this bond with n = 2 and d = 180° (Fig. 4b).
Figure 4: Potential Energy Curves for Two Types of Dihedral
Angles
Non-bonded Interactions
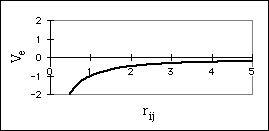
Atoms do not just influence those atoms bonded to it. They also influence atoms near them in space. For example, in liquid water, one water molecule will hydrogen bond with neighboring water molecules. One ion will influence the behavior of another ion, even as far as 10 Å away. A longer flexible molecule can curl around and have atoms interact with each other that are many bonds apart. The dominant interactions controlling these non-bonded influences are van der Waals interactions and electrostatic interactions. (Note: hydrogen bonds are a subset of electrostatic interactions.)
We model van der Waals interactions between two atoms, labeled i and j, using the equation
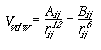 (4)
(4)
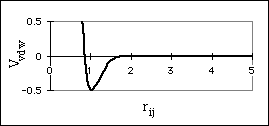
where VvdW is the potential energy due to van der Waals interactions, rij is the distance between the centers of atom i and atom j, and Aij and Bij are constants that depend on the type of atoms interacting. The first term, Aij/rij12, accounts for the repulsion the two atoms experience when their nuclei are too close together, and the second term, Bij/rij6, accounts for the attraction the atoms experience due to induced dipole effects (Aij and Bij are always positive). The sum of the repulsive and attractive terms cause a well to form in the potential energy function (Fig. 5a). This is the preferred interaction distance between the atoms for optimal van der Waals interaction.
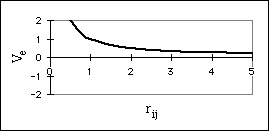
The electrostatic interaction between two atoms, i and j, is modeled using Coulombís Law,
![]() (5)
(5)
where qi is the charge on atom i, qj
is the charge on atom j, rij is the distance between the two atom
centers, and e is the dielectric
constant. If the two atoms have charges of the same sign, this interaction is
repulsive (Fig. 5b). If they have charges of different signs, then the interaction
is attractive (Fig. 5c).
Figure 5: Non-bonded interactions
a) Potential Energy Surface for van der Waals Interaction
b) Potential Energy Surface for Electrostatic Repulsion of Two Like Charges
c) Potential Energy Surface for Electrostatic Repulsion of Two Opposite Charges
The sum total of all the bonded and non-bonded interaction equations and their associated parameters for all atoms in a system constitutes the molecular model of the potential energy used in molecular mechanics. This model is referred to as a force field. Several different force fields have been developed, including CHARMM, AMBER, MM2, and SYBYL. This makes our job easier, as we do not have to figure out the best parameters to use in the above equations; we simply select an existing force field.
In summary, the total potential energy for a molecular system of N atoms, as defined by the equations above, is
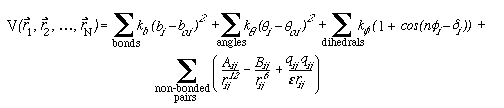 (6)
(6)
where each sum is over all atoms i that participate
in bonds, angles, etc.
Applications of Molecular Mechanics Force Fields
Once the potential energy function of a system is specified
(i.e., a force field chosen), it can be used in various applications to understand
the behavior of molecules. Two common applications, energy minimization
and molecular dynamics, are discussed below.
Energy Minimization
One question that often comes up in computational chemistry is "what is the lowest energy conformation for this molecular system?". Often people are really interested in the lowest free energy state of a molecular system but, since entropy is often difficult to quantify, the lowest potential energy conformation is often found instead. (In quantum mechanics methods, this application is called "geometry optimization".)
The potential energy function (defined by the force field) is used to find conformations of the molecule(s) that give the lowest potential energy. This is akin to a hiker looking around, and progressing to the what is presumably the lowest valley in a mountain range. There are no guarantees it is the lowest valley, it may only be the closest valley. Similarly, minimization algorithms can only guarantee a local minimum will be found, which may or may not be the global minimum.
For an overview of the mathematical methods commonly used in molecular energy minimizations, read p. 135 - 162 in the "Forcefield-Based Simulations" manual from MSI (April 1997).
Molecular Dynamics
Often one is interested in the motion of molecules. This provides a more realistic model of a molecular system that is at a temperature above absolute zero. Once we have the potential energy, V, of a system defined, we can calculate the force on each atom i within that system,
![]() . (7)
. (7)
We also know from Newtonís Equations, that
so, if we know the potential energy function of a system
at time t, we can determine the acceleration of each atom at time t.
If we also know the current position, ![]() of all the atoms, and their current velocities, we can approximately determine
where theyíll be at some later time
of all the atoms, and their current velocities, we can approximately determine
where theyíll be at some later time ![]() from knowledge of their acceleration. Note that
from knowledge of their acceleration. Note that ![]() must be rather small to accurately predict
must be rather small to accurately predict ![]() .
For many molecular systems,
.
For many molecular systems, ![]() is on the order of 1 femtosecond (10-15 sec!).
is on the order of 1 femtosecond (10-15 sec!).
We can start a molecular dynamics simulation by choosing a starting configuration for the molecule(s), and then randomly assign velocities, according to a Boltzmann distribution, to simulate atom motion at a temperature T. Often the starting configuration is the end result of an energy minimization, so that atoms are not too close to one another (if they were, they would repulse each other at very high velocities once the dynamics started, which often causes mathematical convergence problems).
For mathematical details on molecular dynamics simulations,
read p. 169 - 184 in the "Forcefield-Based Simulations" manual from MSI (April
1997).
Questions:
1. If each computer operation simulates 1 fs of molecular dynamics, how many computer operations are required to simulate 1 ns (ns = nanosecond) of molecular dynamics? 1 ms of dynamics?
2. Sketch a plot relating potential energy of a spring to the distance between the masses at each end. Sketch the force as a function of this distance. Using an analogy of the potential energy of a ball on a hillside (i.e., a potential energy surface), which way would the force be directed for different placements of the ball? Is this in agreement with your force plot?
Quantum Mechanics
Unlike molecular mechanics, quantum mechanics is not particularly intuitive. Since we experience life on the order of human size and time frames, we best understand Newtonian physics, which describes how things on this scale work. Quantum physics reduces to Newtonian physics for these large space and time scales. For our little molecular friends, however, quantum physics is the way of the world, so weíll have to stretch our brains to best truly understand how they behave. The details of quantum mechanics will be given in the second semester of physical chemistry, so here we only give you the rudiments you need to get you started in computing electronic structures.
In the early part of this century it was discovered that particles on the size scale of electrons and protons show behavior that can not be explained by the everyday Newtonian physics that you are used to seeing applied to balls, springs, your car, and other objects on a macroscopic scale. For example, it was discovered that electrons and protons behave in a much more probabilistic sense than macroscopic objects. For example, if you throw a ball at a certain angle with a certain initial velocity, then Newtonian physics allows you to calculate with certainty where that ball will be and what its velocity will be at a later time. The same is not true of an atomic level system. Actually, the more you know about the velocity of a quantum mechanical object, the less you can know about its position!
In fact, the only way that we can really understand a quantum mechanical object at all is to think of it not as a particle but as a wave, described by a mathematical function called a wavefunction. The wavefunction for a quantum mechanical object is signified by the Greek letter psi, Y . Now what on earth do we mean when we say that quantum mechanical entities behave in a probabilistic sense and act in a wavelike manner?! Well, it turns out that you have already encountered wavefunctions when you learned about s, p, d and f atomic orbitals. You have probably seen pictures such as those shown below, corresponding to the s, p, and d atomic orbitals. These pictures indicate the region of space in which one is most likely to find an electron in an atom. The darker the shading on the diagram, the more likely you are to find an electron in that place. The functions do not tell you where you are certain to find an electron, they simply map out probabilities! For this reason, the functions plotted here are called probability densities (the probability of finding the electron per unit volume) for an electron. It turns out that they are the square of the wavefunction for the electron, or Y2 (why we need to square the wavefunction is a topic for another day). So, the square of the wavefunction for a quantum mechanical object, Y2, is the probability density for that object.
(Missing stuff here????)
Now a little terminology is in order. An atomicorbital is a one-electron wavefunction, which has little physical meaning until it is squared. The square of the wavefunction is the probability density for the electron. Pictures such as those shown above actually depict the square of the wavefunction, or the square of the orbital. However, many textbooks (especially introductory texts) will blur this distinction and simply describe the pictures above as pictures of atomic orbitals, when in fact they are pictures of probability densities corresponding to atomic orbitals. As computational chemists, you will have to keep in the back of your mind the fact that an atomic orbital is actually a one-electron wavefunction and that wavefunctions are mathematical entities we can use in many ways to find out information about an electron in an atom. One particularly useful application of a wavefunction is the one mentioned here, squaring it to obtain the probability density, i.e., the probable location per volume for the electron.
Letís use an analogy to explore the ideas of wavefunctions and probability densities. Imagine that you called up your best friend every three hours for a week to tell him/her where you were at that moment. Your friend would then make a record of your whereabouts by placing a pin on a map of West Michigan to indicate your location every time you called. At the end of the week, the distribution of pins would be your probability density, or the square of your wavefunction! There would be a big cluster of pins in your bed (assuming you sleep there seven or eight hours a night), a scattering of pins around campus, a big cluster of pins in pchem lab (hee, hee), etc. Someone using this map to find you would have a higher chance of finding you where your probability density is high (where there are more pins), but that doesnít mean that they are guaranteed to find you there! Thatís the idea behind a probability density.
So, you have seen squares of wavefunctions before, in the form of plots of atomic orbitals. As mentioned previously, these wavefunctions are simply functions in three-dimensional space. How are these functions obtained? It turns out that the wavefunction for any system can be obtained from a single equation. This equation, the heart of quantum mechanics, is called the Schrödinger Equation, a differential equation which must be solved for Y , the wavefunction of the system. The time-independent form of the Schrödinger Equation is
HY=EY
where E is a number representing the total energy of the system (kinetic energy plus potential energy) and H is called the Hamiltonian operator, since it operates on the wavefunction. The bold H indicates that it is an operator. An operator is nothing more than something which operates on a function, such a derivative, a second derivative, or the act of multiplying the function by a number or another function. For example, in the following equation
![]() e3x
= 3 e3x
e3x
= 3 e3x
the derivative, ![]() ,
is the operator operating on the function e3x. So, in operator language,
the above equation could also be written as
,
is the operator operating on the function e3x. So, in operator language,
the above equation could also be written as
O![]()
where O = ![]() and f(x) = e3x.
and f(x) = e3x.
In this equation, O is the operator and f(x) is the function on which it is operating, just as in the Schrödinger Equation, H is the operator and Y is the function on which it is operating.
A more detailed version of the Schrödinger equation, which explicitly shows the differential operators involved in H is
![]() .
.
In the expression above, the first term involving the second
derivative represents the kinetic energy of the system. When you take a class
in quantum mechanics you will have the opportunity to explore the reason that
this strange looking operator actually gives the systemís kinetic energy. The
constant multiplying the first term contains Planckís constant, ![]() ,
and the mass of the particle, m. The second term represents the potential energy,
where V(x) is the functional form for the potential energy of the system. The
potential energy operators will vary from system to system. The potential energy
curves of a system are critical to determining its behavior. An example of V(x)
would be the following expression for a simple harmonic oscillator (ball on
a spring) system with spring constant k
,
and the mass of the particle, m. The second term represents the potential energy,
where V(x) is the functional form for the potential energy of the system. The
potential energy operators will vary from system to system. The potential energy
curves of a system are critical to determining its behavior. An example of V(x)
would be the following expression for a simple harmonic oscillator (ball on
a spring) system with spring constant k
V(x) = ![]() kx2
kx2
where x is the displacement from the equilibrium position, or r-r0.
Just as in molecular mechanics, knowing the potential energy function for your system of interest is extremely important in understanding its behavior! Since we are chemists, our systems of interest tend to be atoms and molecules. So, letís think about what the potential energy functions of atoms and molecules should look like. Weíll start with the simplest of all atomic systems, the hydrogen atom. This atom consists of a proton and an electron. Thus the only potential energy term is due to the electrostatic attraction between the proton (a positively charged object) and the electron (a negatively charged object). The expression for the potential energy of two particles with opposite charges is given by Coulombís law
V(x) = ![]() ,
,
where qe is the charge on the electron, qp is the charge on the proton, and rep is the distance between the two particles. When this expression is plugged in for V(x) in the Schrödinger Equation, the expression can be solved exactly for the wavefunction Y by using the mathematical techniques of differential equations. The kinetic energy terms also need to be plugged into the Schrödinger Equation. Both the electron and the proton (nucleus) contribute a kinetic energy. However, the kinetic energy of the proton is usually neglected because the proton, being so much more massive, moves extremely slowly in comparison to the electron. The neglect of the kinetic energy of the proton is called the Born-Oppenheimer Approximation. When the kinetic and potential energy terms are plugged into the Schrödinger Equation it turns out that there are several solutions (called stationary states) to the equation, each yielding a different wavefunction Y . If you were to plot the squares of these wavefunctions on a three dimensional plot, they would look very familiar. They are simply the s, p, d and f atomic orbitals that you have seen before!
In addition to yielding the wavefunctions for the system, the Schrödinger Equation will also produce the energies for each of the different orbitals. These energies can be checked experimentally by doing spectroscopy experiments. Experimental agreement with quantum mechanical predictions for orbital energies is excellent for the hydrogen atom, giving evidence that quantum mechanics, nonintuitive as it may be, does in fact do a good job of describing reality.
Now letís move on to systems that are more complicated than the hydrogen atom. Any atom or molecule is really just a collection of protons, neutrons and electrons. The neutrons donít contribute to the electrostatic potential energy term because they have no charge and thus no electrostatic attractions or repulsions. So the potential energy term for an atomic or molecular system simply consists of the sum of all the Coulombic interactions between all the protons and all the electrons involved in the atom or molecule. You can imagine that, for large atoms or molecules, this potential energy expression can get pretty unwieldy! There are also kinetic energy terms for every particle (each nucleus and each electron), making the overall Schrödinger equation pretty complicated, even when the nuclear kinetic energy terms are left out according to the Born-Oppenheimer Approximation.
The bad news is that the mathematical techniques that we
have available to us do not allow us to solve the Schrödinger
equation analytically (exactly) for any system bigger than the hydrogen atom!
This means that in order to calculate quantum mechanical wavefunctions and energies
for anything of actual chemical interest, one must immediately start making
approximations. A great deal of the work of the quantum chemist and the
computational chemist consists of understanding and choosing between these approximations.
Approximate Methods in Computational Chemistry on Quantum Mechanical Systems
This section will give a very brief overview of the major approximations used in quantum mechanical calculations. This topic will be explored in more detail in CHM 455 (Physical/Computational Chemistry Lab II).
Wavefunctions of more complex atoms and molecules are approximated as products and/or sums of "hydrogenic" wavefunctions. A "hydrogenic" wavefunction is a wavefunction for a single electron subject to electrostatic attraction from a positively-charged core (equivalent to the nucleus in a hydrogen atom). The way this is done is to treat all of the inner electrons and the positively charged nucleus as a charged "blob" with a total charge which is a composite of the charge on the nucleus and the charges on all of the inner electrons. This composite charge will be less than the charge on the nucleus because the inner electrons "shield" the outer electron from the full nuclear charge. The new charge is called the effective nuclear charge, or Zeff. An example of the magnitude of the shielding effect can be seen by considering the sodium atom. Sodium contains eleven protons, so the true nuclear charge is +11. However, ten electrons are shielding the outermost electron from this nuclear charge, and the Zeff for sodium can be calculated to be +1.8. Most computational chemistry methods use Zeff as an adjustable parameter.
Using the approximations above, we would write the wavefunctions for the helium atom (consisting of a nucleus and 2 electrons) as follows
yHe(r1, r2) = y (r1) y (r2)
where r1 and r2 refer to the distance of electrons number one and number two from the nucleus. This wavefunction is the product of the two hydrogenic orbitals y (r1) and y (r2), each with an effective nuclear charge, Zeff. Note that writing yHe in this way is equivalent to considering each electron as occupying its "own" orbital. This approximation is known as the orbital approximation.
A product of wavefunctions is chosen in order to reflect the probabilistic nature of the wavefunction information. Recall that a wavefunction is the square root of a probability density of electron location. Multiplying y (r1) and y (r2) together yields a function which is proportional to the probability density for two electrons acting independently of one another. An analogy can be found if one considers rolling two independent die. By "independent" we mean that one die does not affect the other one. The probability of rolling a six with one die is 1/6. The probability of rolling a six with the other die is also 1/6. However, the probability of rolling a six simultaneously with both die is given as the product of the individual probabilities, or 1/6 x 1/6 = 1/36. Note that the wavefunction for helium obtained by treating the two electrons as statistically independent does not take into account electron-electron repulsion. Realistically accounting for electron-electron repulsion is somewhat involved and is one of the major challenges of computational chemistry!
For molecules, approximate wavefunctions are obtained by adding together wavefunctions from each atom. This technique is known as the LCAO method, standing for Linear Combination of Atomic Orbitals. For example, an approximate wavefunction for the H2 molecule would be
YH2 = c1Y A(r1) YB(r2) + c2Y A(r2) YB(r1).
YA and YB are the hydrogenic wavefunctions for electrons centered on nucleus A and nucleus B respectively. YA(r1) is the hydrogenic wavefunction for electron 1 at a distance r1 from nucleus A and YB(r2) is the hydrogenic wavefunction for electron 2 at a distance r2 from nucleus B. The first term in the equation accounts for the case in which electron 1 is centered on nucleus A and electron 2 is centered on nucleus B. The second term accounts for the case in which electron 1 is centered on nucleus B and electron 2 is centered on nucleus A. In reality, the molecule exists in a superposition of the two situations just outlined, thus the total wavefunction takes this into account with a sum. The coefficients c1 and c2 give the relative weightings of the two possible situations.
For the simple case of the H2, molecule c1 equals c2 . For more complex molecules, the relative sizes of the coefficients multiplying the various atomic orbitals must be determined computationally. This determination involves the computation of various integrals. It can be proven that, if the integral
![]()
can be minimized then Ytrial
is as close as possible to the actual wavefunction of the system. (In this integral,
the ![]() indicates an integral over
all space.) Minimizing this integral leads mathematically to the calculation
of several related integrals. Some of these integrals are shown below
indicates an integral over
all space.) Minimizing this integral leads mathematically to the calculation
of several related integrals. Some of these integrals are shown below
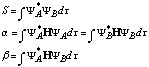
S is called the overlap integral and is a measure of the similarity between the two wavefunctions YA and YB. The function a is called the Coulomb integral and is a measure of the energy of the electron when it is centered on nucleus A or nucleus B. The function b is called the resonance integral and vanishes when the orbitals do not overlap. For complicated systems, the calculation of these integrals can become rather forbidding. This is where the power of computational chemistry comes in. Various methods of approximation are available to calculate these integrals. These levels of approximation are briefly outlined below.
Huckel Method
The Huckel Method makes the most drastic approximations of any method. In this method all a ís are given the same value and all overlap integrals are forced to be zero. Resonance integrals between non-neighbors are neglected. This method works relatively well for conjugated molecules but fails to reliably reproduce experimental data for most other systems.
Semi-empirical Methods
For semi-empirical methods, the Coulomb, resonance and overlap integrals are systematically neglected or approximated with values from spectroscopic data. The input of spectroscopic data accounts for the word "empirical" in the name "semi-empirical". Semi-empirical methods must be used for larger molecules, since a complete calculation of all integrals would be unfeasible given current computer limitations on time and memory.
Ab Initio Methods
Ab initio methods use no empirical data but instead
rely on the computer to actually crank through the integrals. (Ab initio
means "from the beginning".) For this reason, ab initio methods tend
to be more accurate but also much more demanding of computer time and memory.
These methods are excellent for small atoms and small molecules.
References
1. American Heritage Dictionary, 2nd College Ed. (1982). Houghton Mifflin Co., Boston.
2. B. R. Brooks et al. (1983). J. Comput. Chem. 4, 187.