The following well-known experiments serve as a motivation for studying quantum theory. The experimental results cannot be explained using ideas from classical physics.

Blackbody Radiation:

It is well-known that when a body is heated it emits electromagnetic radiation. For example, if a piece of iron is heated to a few hundred degrees, it gives off e.m. radiation which is predominantly in the infra-red region. When the temperature is raised to 1000C it will begin to glow with reddish color which means that the radiation emitted by it is in the visible red region having wavelengths shorter than in the previous case. If heated further it will become white-hot and the radiation emitted is shifted towards the still shorter wave-length blue color in the visible spectrum. Thus the nature of the radiation depends on the temperature of the emitter.

A heated body not only emits radiation but it also absorbs a part of radiation falling on it. If a body absorbs all the radiant energy falling on it, then its absorptive power is unity. Such a body is called a black body.

An ideal blackbody is realized in practice by heating to any desired temperature a hollow enclosure (cavity) and with a very small orifice. The inner surface is coated with lamp-black. Thus radiation entering the cavity through the orifice is incident on its blackened inner surface and is partly absorbed and partly reflected. The reflected component is again incident at another point on the inner surface and gets partly absorbed and partly reflected. This process of absorption and reflection continues until the incident beam is totally absorbed by the body.

The inner walls of the heated cavity also emit radiation, a part of which can come out through the orifice. This radiation has the characteristics of blackbody radiation - the spectrum of which can be analyzed by an infra-red spectrometer.

Experimental results show that the blackbody radiation has a continuous spectrum (shown in the graph).  The intensity of the emitted radiation E_l is plotted as a function of the wavelength l for different temperatures. The wavelength of the emitted radiation ranges continuously from zero to infinity. E_l increases with increasing temperature for all wavelengths. It has very low values for both very short and very long wavelengths and has a maximum in between at some wavelength l_max. l_max depends on the temperature of the blackbody and decreases with increasing temperature.

The shift in the peak of the intensity distribution curve obeys an empirical relationship known as Wien's displacement law:

l_max T = constant.

The total power radiated per unit area of a blackbody can be derived from thermodynamics. This is known as Stefan-Boltzmann law which can be expressed mathematically as:

E = s T⁴,

where s = 5.67 x 10^-8 W m^-2 K^-4 is known as Stefan's constant. 

Note that the total power E radiated is obtained by integrating E_l over all wavelengths. W. Wien proposed an empirical relationship between E_l with l for a given temperature T:

E_l (T) = A exp(-B/lT)/l⁵,

where the constants A and B are chosen arbitrarily so as to fit the experimental energy distribution curves.

But it was later found that the experimental data don't follow Wien's empirical relation at larger wavelengths [See Fig. below ].

>

Wien's theory of intensity of radiation was based only on arguments from thermodynamics not on any plausible model. Considering the radiation system as composed of a bunch of harmonic oscillators Rayleigh and Jeans derived (using thermodynamics) an expression for the emitted radiation E_l:

E_l = (c/4) (8pk_BT/l⁴).

'k_B' is the Boltzman constant (k_B=1.345 x 10^-23 J/K).

The above expression agrees well with the experimental results at long wavelengths but drastically fails at shorter wavelengths. In the limit l -> 0, E_l -> infinity from the expression above, but in the experiments E_l -> 0, as l -> 0. This serious disagreement between theory and experiment indicates the limitations of classical mechanics.

Max Planck later derived an expression for the emitted radiation using quantum mechanics. He made a bold new postulate that an oscillator can have only energies which are discrete, i.e., an integral multiple of a finite quantum of energy hf where h is Planck's constant (h= 6.55 x 10^-34 J.s) and f is the frequency of the oscillator. Thus the energy of the oscillator is,

E = nhf,

where n is an integer or zero. Planck further assumed that the change in energy of the oscillator  due to emission or absorption of radiant energy can also take place by a discrete amount hf. Since radiation is emitted from the oscillators, and since according to Planck, the change in energy of the oscillators can only take discrete values, the energy carried by the emitted radiation, which is called a photon, will be hf, and that is also equal to the loss of energy of the oscillator. Again, this is also the energy gain of the oscillator when it absorbs a photon. Based on these ideas Planck derived the expression for the energy distribution of blackbody radiation:

E_l = (c/4) (8phc/l⁵)(1/[exp(hc/lk_BT) - 1]).

Rayleigh-Jean's expression and Wien's displacement law are special cases of Planck's law of radiation. Planck's formula for the energy distribution of blackbody radiation agrees well with the experimental results, both for the long wavelengths and the short wavelengths of the energy spectrum.

Please click on the simulation below to see nice interactive demonstration of the physics of Blackbody radiation.

Simulation on Blackbody Radiation

Back to Top

Photoelectric Effect:

Planck's postulate regarding the discrete nature of the possible energy states of an oscillator marked a radical departure from the ideas of classical physics. According to the laws of classical mechanics, the energy of an oscillator can vary continuously, depending only on the amplitude of the vibrations - this is in total contrast to Planck's hypothesis of discrete energy states of an oscillator. Photoelectric effect is another classic example which can not be explained with classical physics. Einstein was awarded Nobel prize for his explanation of the physics of photoelectric effect.

The basic experiment of photoelectric effect is simple. It was observed that a metal plate when exposed to ultraviolet radiation became positively charged which showed that it has lost negative charges from its surface. These negatively charged particles were later identified to be electrons (later named photoelectrons). This phenomenon is known as photoelectric effect.

Please check out the physics applet below which shows the effect  of light on various metals.

Simulation on Photoelectric effect

The main results of the experiment can be summarized as follows:

On exposure to the incident light, photoelectrons with all possible velocities ranging from 0 upto a maximum v_m are emitted from the metal plate. When a positive potential is applied to the collector (which collects the emitted photoelectrons), a fraction of the total number emitted is collected by the collector. This fraction increases as the voltage is increased. For potentials above about +10 volts, all the electrons emitted by the light are collected by the collector which accounts for the saturation of the photoelectric current [Figs. (a) and (b) below].

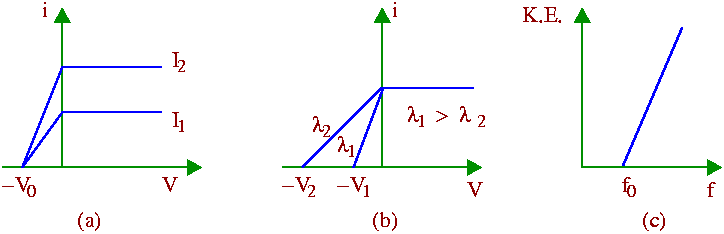
On the other hand, when a negative retarding potential is applied on the collector, the lower energy electrons are unable to reach the collector so that the current gradually decreases with increasing negative potential. Finally for a potential -V₀ (known as the stopping potential), the photoelectrons of all velocities upto the maximum v_m are prevented from reaching the collector. At this point, the maximum kinetic energy of the emitted electrons equals the energy required to overcome the effect of the retarding potential - so we can write

mv_m²/2 = eV₀.

Conclusion from the experimental results:

(1) The photoelectric current depends upon the intensity of the light used. It is independent of the wavelength of the light [See Fig. (a) above].

(2) The photoelectrons are emitted with all possible velocities from 0 upto a maximum v_m which is independent of the intensity of the incident light, but depends only on its wavelength (or frequency). It is found that if f is the frequency of the light used, then the maximum kinetic energy of the photoelectrons increases linearly with f [See Figs. (b) and (c) above ].

(3) Photoelectron emission is an instantaneous effect. There is no time gap between the incidence of the light and the emission of the photoelectrons.

(4) The straight line graph showing the variation of the maximum kinetic energy of the emitted electrons with the frequency f of the light intersects the abscissa at some point f₀. No photoelectron emission takes place in the frequency range f<f₀. This minimum frequency f₀ is known as the threshold frequency. Its value depends on the nature of the emitting material [See Fig. (c) above].

Breakdown of Classical Physics:

According to classical physics -

(a) Light is an electromagnetic wave - the intensity of light is determined by the amplitudes of these electromagnetic oscillations. When light falls on an electron bound in an atom, it gains energy from the oscillating electric field. Larger the amplitude of oscillations, larger is the energy gained by the emitted electron - thus energy of the emitted electrons should depend on the intensity of the incident light. This is in contrast to what has been observed in experiment (point 2 above).

(b) According to the electromagnetic theory, the velocity of the emitted electrons should not depend on the frequency of the incident light.  Whatever may be the frequency of the incident light, the electron would be emitted if it gets sufficient time to collect the necessary energy for emission. So the photoelectric emission is not an instantaneous effect. These are in contrary to points 3 and 4 above.

(c) Finally, the incident electromagnetic wave acts equally on all the electrons of the metal surface. There is no reason why only some electrons will be able to collect the necessary energy for emission from the incident waves. Given sufficient time, all electrons should be able to collect the energy necessary for emission. So there is no reason why the photoelectric current should depend upon the intensity of the incident light. However, this is again in contrary to the observed facts (point 1 above).

Einstein's light quantum hypothesis and photoelectric equation:

We have seen from above that the maximum kinetic energy of the emitted photoelectrons increases linearly with the frequency of the incident light. In terms of equation we have

mv_m²/2 = eV₀ = af - W

where a and W are constants.  W is known as the work function of the emitting material. The constant a was determined experimentally and is found to be equal to the Planck's constant h. We can then rewrite the above equation as -

mv_m²/2 = eV₀ = hf - W.

For the special value of f = f₀ = W/h, the K. E. of the emitted photoelectrons becomes zero. So there will be no photoelectron emission if f < f₀. f₀ is the threshold frequency. The equation,

mv_m²/2 = eV₀ = hf - hf₀

is known as the famous Einstein's photoelectric equation.

Einstein used the quantum hypothesis of Planck to explain the photoelectric effect. He postulated that light is emitted from a source in the form of energy packets of the amount hf known as the light quantum or photon. This is known as Einstein's light quantum hypothesis.

When a photon of energy hf falls on an electron bound inside an atom, the electron absorbs the energy hf and is emitted from the atom provided that hf is greater than the energy of binding of the electron in the atom which is equal to the work function W of the metal. The surplus of energy (hf - W) is taken away by the electron as its kinetic energy. Obviously if hf < W, i.e. f<f₀, no photoelectric emission can take place. This explains the existence of the threshold frequency.

Furthermore, according to Einstein's theory, larger the number of photons falling on the metal, greater is the probability of their encounter with the atomic electrons and hence greater is the photoelectric current. So the increase of photoelectric current with the increasing light intensity can be easily explained.

Finally, as soon as the photon of energy hf > W falls on an electron, the latter absorbs it and is emitted instantaneously.

Note that Einstein's light quantum hypothesis postulates the corpuscular nature of light in contrast to the wave nature. We will talk about this wave-particle duality later on in this course.

Back to Top

Compton Effect:

The discovery of Compton scattering of x-rays provides direct support that light consists of pointlike quanta of energy called photons.

The experiment:

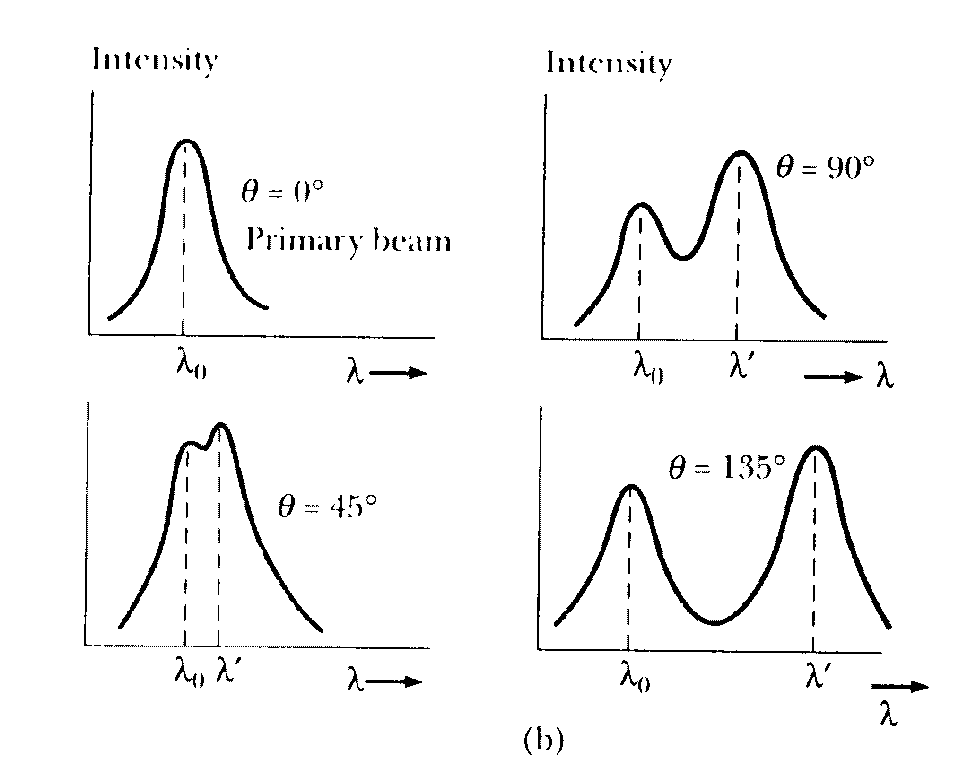
A schematic diagram of the apparatus used by Compton is shown in the Figure below. A graphite target was bombarded with monochromatic x-rays and the wavelength of the scattered radiation was measured with a rotating crystal spectrometer. The intensity was determined by a movable ionization chamber that generated a current proportional to the x-ray intensity. Compton measured the dependence of scattered x-ray intensity on wavelength at three different scattering angles of 45^o, 90^o, and 135^o. The experimental intensity vs. wavelength plots observed by Compton for the above three scattering angles (See Fig. below) show two peaks, one at the wavelength l of the incident x-rays and the other at a longer wavelength l'. The functional dependence of l' on the scattering angle and l was predicted by Compton to be:

l' - l = (h/m_ec)[ 1- cosq ] = l₀ [ 1- cosq ].

The factor l₀=h/m_ec, also known as Compton wavelength can be calculated to be equal to 0.00243 nm.

The physics of Compton effect:

To explain his observations Compton assumed that light consists of photons each of which carries an energy hf and a momentum hf/c (as p = E/c = hf/c). When such a photon strikes a free electron the electron gets some momentum (p_e) and kinetic energy (T_e) due to the collision, as a result of which the momentum and energy of the photon are reduced.

Considering energy and momentum conservation (For the detail derivation please click here) one can derive the change in wavelength due to Compton scattering:

l' - l = (h/m_ec)[ 1- cosq ].

Note that the result is independent of the scattering material and depends only on the angle of scattering.

The appearance of the peak at the longer wavelength in the intensity vs. wavelength curve is due to Compton scattering from the electron which may be considered free, since its energy of binding in the atom is small compared to the energy hf of the photon. The appearance of the other peak at the wavelength of the incident radiation is due to scattering from a bound electron. In this case the recoil momentum is taken up by the entire atom, which being much heavier compared to the electron, produces negligible wavelength shift.

Conclusion:

Compton effect gives conclusive evidence in support of the corpuscular character of electromagnetic radiation.

Please check out the simulation below which shows Compton scattering.

Simulation on Compton Scattering

Back to Top

© Kingshuk Majumdar (2000)