Circle Packing
Summer 2018
Since coming to GVSU I have been involved in conducting research with undergraduates. I have mentored 15 summer projects resulting in several publications and awards for my students. In 2010 I became the co-director of the Research Experiences for Undergraduates (REU) Site in mathematics at GVSU. This is the latest in a series of such grants for GVSU dating back to 2000. Below is a description of one of my projects for summer 2018. This was also the subject of the summer research with undergraduates in several previous summers.
Suppose you have seven cans of soda pop, what is the smallest box with a square cross section that can hold them standing upright in a single layer? By examining the cross section of the box, you can see that this is equivalent to determining the smallest square that contains seven equal and non-overlapping circles. The optimal solution is the arrangement below. You might think you can rearrange the circles in to a more dense arrangement so that there is no `free` circle (like the one in the upper left corner), but you cannot. This is a result due to J. Schaer and R. Graham from 1965.
Overview and Introduction

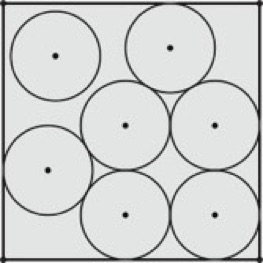
Notice how the circles are equal in diameter and non-overlapping and are contained in a square -- that is, they form an equal circle packing in a hard-boundary square. Over past summers, we have studied an equivalent problem to the soda pop can packing one. We let the equal circles expand, while fixing the size of the container. More formally we sought to determine the largest possible common diameter of a fixed number of equal circles that form a packing in some kind of container. This is a problem in discrete geometry and, in the case of a hard boundary square, optimal arrangements have been proven for at least 20 equal circles and there are conjectured optimal arrangements for all n up to over 10000 equal circles. Packing of equal objects in other hard-boundary containers have also been studied.
This research project examines packings of circles in containers other than a hard-boundary square. The main focus of this project will be to consider spaces obtained from square (or more generally parallelograms) where the top and bottom and the left and right sides are identified. One such space is called a square flat torus and is represented by the dark square in the picture below which contains seven circles. Can you count the seven circles?
This is has been proven [Musin, Nikitenko] to be one of three equal density arrangements of seven equal circles on a square flat torus. Included in this picture, in addition to the seven equal circles and the torus, is the packing graph associated to this packing. A packing graph is a graph where the vertices are the centers of the circles and the edges connect tangent circles. This graph comes naturally with an embedding on the torus and its properties are very important in the approach that we will use to study these packing.
In past summer research, we studied equal circle packings on a flat Klein bottles and flat tori. This summer we are going to extend this to not-necessarily-equal circle packings on a square torus. We will start with two not-necessarily-equal circles. In the image below there are two unequal circles on a square torus. Can you see the edges of the square torus onto which the circles are packed? (Hint: the edges are not solid lines.)
What Will This Research Involve?
Desirable Experiences For Applicants
What this project is NOT...
How To Apply
Applicants should like to analyze geometric situations -- working with lines, angles and geometric objects will be important to success of this research. The ideal applicant will geometrically inclined. The desirable experiences for applicants to this project are a positive attitude toward geometric ideas and a bit of geometric background. The background could be just that you liked geometric reasoning in the classes you have taken (like calculus or linear algebra) or it could be your enjoyment of any kind of geometry course you have taken.
Applied. Yes, I really DO NOT care about applications of this to packing anything real. I enjoy the mathematical side of this and not anything practical that may come out of this. (There could be applications of this -- I do not know and I’m not looking for them.)
For application information and instructions, please visit the GVSU Summer Mathematics REU home page.
1) Exploring packings to find candidate optimal arrangements. Some of this might be done using the program that I wrote during my sabbatical at Cornell University.
2) Analyzing geometric situations, like finding the analytic coordinates of the centers of the circles in the packings above.
The goal of the research is to prove that we have all the optimal arrangements for a fixed small number of circles in a container or class of containers. Further we also need to prove that the discovered arrangement are, in fact, optimal. We will begin the summer by reviewing techniques used by previous summer research students (this will take at most a few days).
This summer research will involve formulating and proving theorems about packings. The primary tools/techniques/activities involved in this are the following:
