THE MANDELBROT SET
The Mandelbrot set M
arises from the family of quadratic functions 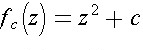 ,
where
z is a complex input and c is a complex parameter.
One way to define this set is to fix a value of c=c1+i*c2
and compute the orbit of z=0 under
,
where
z is a complex input and c is a complex parameter.
One way to define this set is to fix a value of c=c1+i*c2
and compute the orbit of z=0 under 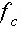 as follows:
as follows:
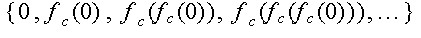 .
.
If this set of complex numbers is bounded in the complex
plane, then c belongs to M, and vice versa.
The significance of z=0 is that it is the critical
value of 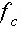 .
.
A second, equivalent, way to define
the Mandelbrot set is given in terms of filled Julia sets. If one fixes
a value of c=c1+i*c2, the filled Julia
set Kc is the set of complex inputs z for which
the orbit
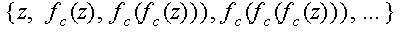
is bounded in the complex plane. Note that while the Mandelbrot
set M is a set in the c-plane, each filled
Julia set Kc, which depends upons the value of c,
is a set in the z-plane. It ends up that the Mandelbrot set M consists
precisely of those values of c for which Kc
is connected.
The Java applet below draws in black the
Mandelbrot set on the viewing window [xmin, xmax] x [ymin, ymax].
The coarseness level, an integer between 1 and 9 inclusive,
determines the quality of the image. A coarseness level of 9 produces the
highest quality image but takes longer to produce.
-
To change the viewing window and/or the coarseness level,
edit the desired fields and push the "redraw" button.
-
To zoom in at a point on the graph, click the mouse at the
desired point, and then hit the "zoom" button. (The zoom factor is 4 in
both the horizontal and vertical directions.)
-
To view the filled Julia set Kc associated with
a particular value of c = (c1,c2),
click the mouse at the desired value of c, and then hit the
"julia" button.
-
The "reset" button draws the Mandelbrot set using the default
coarseness level (7) and the default viewing window ([-2, .5] x [-1.25,
1.25]).
-
The "redraw" button redraws the Mandelbrot set using the
current settings.
-
By changing alpha and beta, you may view Mandelbrot sets associated
with other
binary number systems number systems.
A tip for zooming: The applet uses a standard escape time
algorithm to determine whether each point (c1,c2)
belongs in the Mandelbrot set. For points belonging to the Mandelbrot set,
this algorithm takes longer than it does for points not in the set.
Consequently, when you zoom, the more points in black (i.e. in the Mandelbrot
set) that fall within your new window, the longer the time needed to create
the new image.
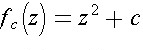 ,
where
z is a complex input and c is a complex parameter.
One way to define this set is to fix a value of c=c1+i*c2
and compute the orbit of z=0 under
,
where
z is a complex input and c is a complex parameter.
One way to define this set is to fix a value of c=c1+i*c2
and compute the orbit of z=0 under 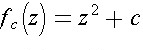 ,
where
z is a complex input and c is a complex parameter.
One way to define this set is to fix a value of c=c1+i*c2
and compute the orbit of z=0 under
,
where
z is a complex input and c is a complex parameter.
One way to define this set is to fix a value of c=c1+i*c2
and compute the orbit of z=0 under ![]() as follows:
as follows:
![]() .
.![]() .
.
![]()