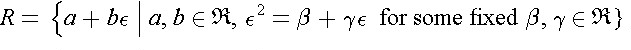A binary number system is any two-component number system of the form

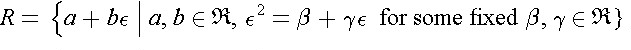Here  denotes the set of real numbers. Binary numbers are added componentwise and are multplied together using the "foil method" together with the identity .

Three very special examples of binary number systems are given by the following.
 

• In this case , which of course yields the complex number system.
• Hence . This case yields what is known as the perplex number system.
• Hence . This case yields what is known as the dual number system.

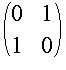Both the perplex numbers and dual numbers can be identified with subrings of the ring of two by two real matrices. For example, the perplex number   can be identified with the two by two matrix , whose square is the identity matrix. Under the identification, the arbitrary perplex number 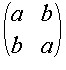 is identified with the two by two matrix .

In a similiar manner, the dual number   can be identified with the two by two matrix , whose square is the zero matrix. Under this identification the arbitrary dual number  is identified with the two by two matrix .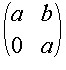
 Back to Mandelbrot Viewer