The Strange World of the
Hausdorff Metric Geometry
XIII. What
is Special about the
Number 19?
As mentioned in the last section, we can find
sets A and B so that the number of elements at each location between A and B can be any Fibonacci or Lucas number, or any integer between 1
and 18. Now we investigate the number 19.
Through an
exhaustive argument in which we checked all finite configurations X that could possibly satisfy #(X) = 19, in the 2004 GVSU REU, Kris Lund, Patrick Sigmon, and I showed that
there is no finite configuration XF
for which #(XF) = 19 (see
[3]). The question remains, however, if there is an infinite configuration X for which #(X) = 19. The answer turns out to be no. The Finite Conversation
Algorithm and the Configuration Construction Theorem (described in the next
section) show us that given any infinite configuration X so that #(X) is finite, we can construct a
corresponding finite configuration XF
with #(XF) = #(X). Therefore, infinite configurations
provide no additional possibilities beyond the ones provided by finite
configurations. We conclude the surprising result that there are no
configurations X for which #(X) = 19. To discuss the next theorems we
need to review subspace topologies.
Subspace Topology and Elements Satisfying ACB.
Let (X,T) be a topological space, and let C be a subset of X. The subspace topology of C, denoted TC, is the set {O ∩ C : O is in T}. If U is in TC, we say that U is a relatively open set.
The subspace topology TC on a set C is a topology on C. We will eventually be able to connect the subspace topology of C with the elements at each location between A and B, but we need to make several more definitions in order to have the necessary tools to make this connection.
Let A and C be elements in H(Rn) and let a be an element of A. We define the adjacency set of a relative to C as the set
[a]C = {c in C : dE(a, c) = h(A,B)}.
We will let [A]C denote the set {[a]C : a in A}.
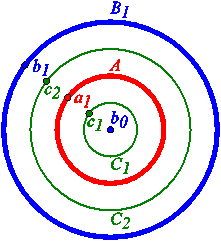
Figure 7
For example, in the configuration shown in Figure 7, we can see that [a1]C = {c1, c2} and [b0]C = C1.
Let [A, B] be a configuration and C be the largest element in H(Rn) satisfying ACB at a given location.
· Let qA : C → [A]C be defined by qA(c) = [a]C, where c is in [a]C.
· Let qB : C → [B]C be defined by qB(c) = [b]C, where c is in [b]C.
For example, consider the configuration X in R2 defined by A = {(0,0)} and B = {(x,y) : x2 + y2 = 1}. The only element between A and B that is 1/2 units from A is the set C = {(x,y) : x2 + y2 = 1/4}. Then [(0,0)]C will be the set of all points on C, since (0,0) is adjacent to every one of these points. Also, for any b in B, we can see that [b]C will be the single point on C that intersects a line drawn between b and the origin. For any point c in C, we have qA(c) = [(0,0)]C. The adjacency set given by qB(c) will be different for every c.
A straightforward computation shows that qA and qB are both well-defined and onto. Now we can begin to define the function that will take an element of the subspace topology of C to an element between A and B.
Define Ω as the set of all U in UC such that
· for all [a]C in qA(A), there exists c in [a]C such that c is not in U
· for all [b]C in qA(B), there exists c in [b]C such that b is not in U
Now let Z be the set of all C* such that C* satisfies AC*B with h(A,C*) = h(A,C). Note that every C* must be a subset of C [2].
Finally, define f : Ω → Z by f(U) = C - U.
As an example, let A = {a1, a2}, B = {b1, b2}, and C = {c1, c2, c3} as shown in Figure 8. We can see that [A, B] is a configuration.
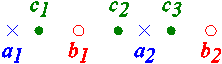
Figure 8
For this configuration, we have Ω = {Ø, {c2}}. It would be impossible to have c1 in any U in Ω because qA(c1) = [a1]C = {c1}, which would mean that there would not exist another c in [a1]C such that c is not in U. A similar argument shows that c3 cannot be in any U in Ω. In this example, f(Ø) = C and f({c2}) = {c1, c3}, both of which lie at the location shown between A and B.
In the next section we introduce the Finite
Conversion Algorithm and the Configuration Construction Theorem.