Resources for Teaching
Complex Variables
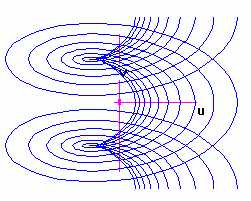
Riemann Surface for the Logarithm Function.
Created using F(z) for Windows
This web site contains
resources for individuals teaching an introductory, undergraduate course
in complex variables. Over the years I've tried to create a series of activities,
F(z) files, and Maple worksheets that can be used to create an active classroom
learning atmosphere that replicates what I do in my calculus classes and
that gives meaning to the various concepts from complex analysis.
Site Contents:
[Activities] [ F(z) Programs]
[Links to other sites]
[Bibliography]
Activities
You'll need the free Adobe
Acrobat Reader to view most of these activities.
-
Euler's
Identity, the Complex Exponential, and the Polar Form, Revisited:
This is a brief activity in which students derive Euler's identity using
Taylor series. They then plot a partial sum of the resulting series for
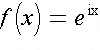 as a vector using the tip to tail method of vector addition. A "spraling
in" of the vectors illustrates the convergence of the series. Adapted from
Visual
Complex Analysis.
as a vector using the tip to tail method of vector addition. A "spraling
in" of the vectors illustrates the convergence of the series. Adapted from
Visual
Complex Analysis.
-
Mapping
Properties of Complex-valued Functions In this activity students use
F(z) and work in small groups to investigate mapping properties of various
functions. Each group is given a particular function and a particular set
of domains and is asked a series of questions that focus on mapping properties
and that seek to compare and contrast properties of the function with its
real counterpart. Each group then presents its findings to the rest of
the class in the computer lab.
-
The
Amplitwist Principle This is a term I believe is due to Tristan Needham.
The idea of this activity is for students to discover the idea that a complex-valued
function is differentiable at a point provided it has a well-defined "amplitwist"
there. An amplitwist is a composition of an amplification and a "twisting"
or rotation. Under this identification, the derivative may be thought of
locally as a linear transformation, and the tangent line approximation
from calculus becomes an affine transformation. An F(z) file ( AMPLITW.FZW
) accompanies this activity.
-
The Polya Vector Field is a useful tool for giving meaning to the basic
concepts of complex varibles and has been written about extensively by
Bart Braden. The idea is that one may associate to the complex-valued function
 the vector field
the vector field  .
A plot of this vector field allows for visualization of a variety of ideas.
.
A plot of this vector field allows for visualization of a variety of ideas.
-
Two student papers from 1998 that describe some of the properties of the
Polya Field.:
-
Brief activity on matching a Polya Field to its function formula.
Polya
Field Example
-
Maple activity on differentiability and the Polya Field. If a function
is analytic in some region, the divergence and curl of its associated Polya
Field is identically zero. Hence, the Polya field has no sources and sinks
and is irrotational. Maple
file (save by holding down shift/leftmouse simultaneously) HTML
version of Maple file
-
Interpreting
the Contour Integral This is an activity on the contour integral and
the Polya Field. The real and imaginary parts of a contour integral measure
the "flow" and "flux", respectively, of the Polya field along the contour.
-
Maple activity on using the Polya Field and animation to visualize Taylor
series convergence. I have students use this file in order to determine
whether the Taylor series for a particular function converges at various
points within a certain region. The objective is for students to discover
on their own that the radius of convergence of a Taylor series is the distance
from the center of the series to the nearest singularity of the function.
Maple
file (save by holding down shift/leftmouse simultaneously) HTML
version of Maple file (Note that the HTML version does not display
the animation.)
-
An
Overview of the Contour Integral Class handout summarizing some properties
of the contour integral.
-
Cauchy's
Theorem and Curve Deformation: In this activity students calculate
the contour integral along a circle of radius two centered at the origin
for a function having two poles inside this circle. At this point the students
have not seen the Cauchy integral formula; instead they perform a partial
fraction decomposition and use the fact that
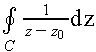 , where C is a circle, is zero if z0 is outside this circle and is
, where C is a circle, is zero if z0 is outside this circle and is 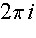 if z0 is inside the circle. The circle is then moved so that it contains
one singularity and then again so that it contains no singularities, and
new values of the integral are quickly recalculated. An F(z) animation
(using DEFORM.FZW
) illustrates that as the circle moves in general, the contour integral
can only take on three different values.
if z0 is inside the circle. The circle is then moved so that it contains
one singularity and then again so that it contains no singularities, and
new values of the integral are quickly recalculated. An F(z) animation
(using DEFORM.FZW
) illustrates that as the circle moves in general, the contour integral
can only take on three different values.
Back to Table of Contents
For each F(z) file you wish to obtain, click on the file name. You should
see a text file in your browser. Save this text file to disk, making sure
to include the ".fzw" suffix at the end of the name you choose. Then open
the file from within the F(z) program.
-
COSINE.FZW:
Illustrates the image under the cosine map of horizontal lines, vertical
lines, and rectangular regions. Based upon an idea from Needham's book
above.
-
POLYAFLD.FZW:
Draws the Polya Vector Field for the function f(z)=z^2. The Polya Field
has been discussed extensively by Braden and allows for visualization of
such ideas as differentiability (related to the divergence and curl of
the field), the value of contour integrals (related to flux and flow along
the contour), and the argument principle.
-
DERIVDEF.FZW:
Investigates differentiability near the origin for the function f(z)=z^2+z^5/norm(z^4).
Different paths of approach are animated to show that (f(z)-f(0))/z has
no limit as z approaches zero.
-
AMPLITW.FZW:
File that accompanies the activity The Amplitwist Principle. The
"amplitwist" principle is the complex analog of the calculus idea of local
linearity or linearization. If a function is differentiable at a point,
then locally it behaves as an affine transformation of the plane.
-
AVGVAL.FZW:
Uses Gluchoff's interpretation of the contour integral as a vector average.
The integral of a function f along an arc gamma is the length of the gamma
multiplied by the average along gamma of f times the unit tangent vector.
-
DEFORM.FZW:
File that accompanies the activity Cauchy's Theorem and Curve Deformation.
Animates
the value of a contour integral as the location of the contour changes.
The contour is a simple circle with changing center, and the integrand
is a simple rational function with two poles.
-
C_INTFRM.FZW:
Allows for numerical approximation of an integral having integrand of the
form f(z)/(z-z0). Using the mouse to estimate the value of the integral,
together with a graphing calculator to estimate f(z0), students can discover
the Cauchy Integral Formula..
-
DISCCONV.FZW:
Allows for discovery of the disk of convergence for the Taylor series of
f(z)=1/(z^2+2) centered about the origin. The 10th and 20th partial sums
of the Taylor series are plotted as vector fields. Inside the disk of radius
sqrt(2) centered at the origin, the vector fields appear similar. Outside
this same disk they appear quite different.
-
UNIFCONV.FZW:
Plots the error involved in using the partial sum of the Taylor series
about z=0 for the function f(z)=1/(1-z). The errors are plotted using domains
of concentric circles of increasing radii. As the radii of the circles
approach 1, the error grows in magnitude, illustrating how convergence
of the Taylor series is slowest near the boundary of the disk of convergence.
I ask the students to do what they can to reduce the error. Most will simply
increase the number of terms used in the partial sum, which of course doesn't
really help. Usually a few students recognize the need to reduce the outer
radius to a number slightly less than 1. This activity serves as a nice
lead in to the idea of uniform convergence.
-
REALINT.FZW:
Investigates the integral of f(x)=cos(x)/(1+x^2) along the real line. The
value of the integral f along a simple closed contour consisting of a segment
along the real axis and a semicircle in the upper half plane are each independently
illustrated. As the size of the contour increases, animation illustrates
how the contribution to the value of the integral coming from the semicircle
goes to zero.
-
RIEMSURF.FZW:
Uses the 4-D graphing features of F(z) to create the Riemann surface for
the logarithm.
Click here
for
a detailed booklet in PDF format that gives instructions on how some of
these F(z) files were created.
Back to Table of Contents
Some Other Web Sites Related to the Teaching of Complex
Variables:
Back to Table of Contents
Bibliography
-
Beardon, Alan Iteration of Rational Functions , Springer-Verlag.
-
Braden, Bart, "The Vector-Field Approach in Complex Analysis," from Visualization
in Teaching and Learning Mathematics , MAA Notes #19, 1990, pp. 191-196.
-
Braden, Bart, "Polya's Geometric Picture of Complex Contour Integrals,"
Mathematics
Magazine , Volume 60, 1987, pp. 321-327.
-
Braden, Bart, "Picturing Functions of a Complex Variable," College Mathematics
Journal , Volume 16, 1985, pp. 63-72.
-
Devaney, Robert, An Introduction to Chaotic Dynamical Systems ,
Addison-Wesley.
-
Gluchoff, Alan, "Complex Power Series-A Vector Field Visualization," Mathematics
Magazine , Volume 66, 1993, pp. 189-191.
-
Gluchoff, Alan, "A Simple Interpretation of the Complex Contour Integral,
The
American Mathematical Monthly , Volume 98, 1991, pp. 641-644.
-
Matthews, John and Howell, Russell, Complex
Analysis for Mathematics and Engineering , Jones and Bartlett.
-
Needham, Tristan, Visual Complex
Analysis , Oxford University Press.
-
Needham, Tristan, "The Geometry of Harmonic Functions," Mathematics
Magazine , Volume 67, 1994, pp. 93-108.
-
Newton, Tyre and Lafaro, Thomas, "On Using Flows to Visualize Functions
of a Complex Variable," Mathematics Magazine , Volume 69, 1996,
pp. 28-33.
-
Polya, George and Latta, Gordon, Complex Variables , Wiley, 1974.
Back to Table of Contents
This site is maintained by
Paul Fishback
Department of Mathematics
Grand Valley State University
Allendale, MI 49401
fishbacp@gvsu.edu
Last updated on 12/17/01.


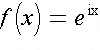 as a vector using the tip to tail method of vector addition. A "spraling
in" of the vectors illustrates the convergence of the series. Adapted from
Visual
Complex Analysis.
as a vector using the tip to tail method of vector addition. A "spraling
in" of the vectors illustrates the convergence of the series. Adapted from
Visual
Complex Analysis. .
A plot of this vector field allows for visualization of a variety of ideas.
.
A plot of this vector field allows for visualization of a variety of ideas.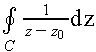 , where C is a circle, is zero if z0 is outside this circle and is
, where C is a circle, is zero if z0 is outside this circle and is